Primzahlen von Euklid bis heute
Ernst-Ulrich Gekeler, Universität des Saarlandes
(1) Was wissen wir über Primzahlen?
(2) Wann tritt der Begriff zum ersten Mal auf?
(3) Wer hat zu welcher Zeit was über Primzahlen gewußt?
Klare Antwort zu (2): Euklid, Elemente, Bücher VII-IX (um 300 v. Chr.)
Wenige schwache Hinweise vorher:
Euklid (ca. 325-265 v.Chr.)

Elemente, Bücher VII-IX
"Eine Primzahl ist eine Zahl, die sich nur durch die Einheit messen läßt."
Elementare Teilbarkeitslehre:
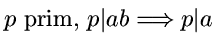 oder
oder (trotzdem keine explizite Erwähnung der Eindeutigkeit der Primfaktorzerlegung)
Bemerkenswert:
in der (für uns!) äquivalenten Form des unendlichen Abstiegs in VII,31
(. Gilt :"
", so ist
.)
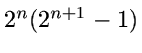 ist "vollkommen" (d.h., sie stimmt mit der Summe ihrer echten Teiler überein),
falls der zweite Faktor prim ist.(IX, 36: Abschluß und Höhepunkt
der arithmetischen Bücher)
ist "vollkommen" (d.h., sie stimmt mit der Summe ihrer echten Teiler überein),
falls der zweite Faktor prim ist.(IX, 36: Abschluß und Höhepunkt
der arithmetischen Bücher)


1537 Practica Arithmeticae generalis
1545 Ars magna sire de regulis algebraicis
etwas später Ars magna arithmeticae
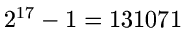 und
und 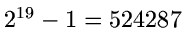 sind prim
sind prim
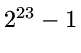 ,
, 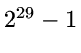 ,
, 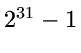 ,
, 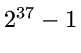 behauptet, was aber für
behauptet, was aber für
Methode: Aufstellen der ersten ausführlichen Primzahltabellen
(![]() ), dann
Probedivision.
), dann
Probedivision.
Wieso Zahlen der Form ![]() ,
, ![]() prim?
prim?
(a) ![]() ,
, ![]() nicht prim:
nicht prim:
nicht prim!
(b) ![]() prim. Jeder Teiler
prim. Jeder Teiler ![]() von
von ![]() hat die Form
hat die Form ![]() (Fermat 1640)
(Fermat 1640)
deshalb kommen nur wenige Zahlen als Teiler vonin Frage, z.B. für
nur
,
,
,
Die ![]() heißen Mersenne-(Prim)zahlen nach dem Abbé
heißen Mersenne-(Prim)zahlen nach dem Abbé
Marin Mersenne (1588-1648),

der 1640 die Primalität von ![]() für
für ![]() behauptet hat.
behauptet hat.
(Falsch für ![]() ,
dagegen richtig auch für
,
dagegen richtig auch für ![]() .)
.)
 .
.
.
.
geben "einfachen" Test auf Primalität von ![]() für große Primzahlen
für große Primzahlen ![]() .
Seither fast alle Primzahlrekorde durch Mersenne-Primzahlen.
.
Seither fast alle Primzahlrekorde durch Mersenne-Primzahlen.
Lucas 1876: 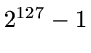 (39 Stellen) ist prim.
(39 Stellen) ist prim.
Pierre de Fermat (1601-1665)

Wichtige Beiträge zur Entwicklung des Differential- und Integralkalküls, zur Variationsrechnung, Geometrie, Zahlentheorie: quadratische Formen, diophantische Gleichungen, Primzahlen...
Z.B.
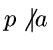 .
Dann
.
Dann("Kleiner" Satz von Fermat)
keine "nichttrivialen" Lösungen 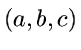 in ganzen Zahlen (?)
in ganzen Zahlen (?)
("Großer" Satz von Fermat)
Leonhard Euler (1707-1783)

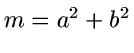 ,
und
,
und 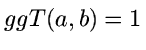
(Beispiele für große Primzahlen, Widerlegung von Fermats Behauptung der Primalität von)
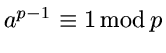
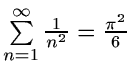
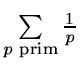
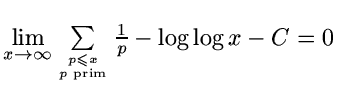 ,
, Goldbach-Vermutung
Christian Goldbach (1690-1764), Freund, Förderer, Korrespondent von Euler
"Jede natürliche Zahl ![]() ist Summe dreier Primzahlen" (?)
ist Summe dreier Primzahlen" (?)
(Goldbach 1742 in Brief
an Euler)
Äquivalent (Euler im Antwortbrief):
"Jede gerade Zahl ![]() ist Summe zweier Primzahlen"
ist Summe zweier Primzahlen"
Bisher unbewiesen!
Abgeschwächte Formen können bewiesen werden, z.B.:
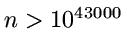 ist Summe von höchstens 4 Primzahlen (Vinogradov 1937, Chen-Wang 1989)
ist Summe von höchstens 4 Primzahlen (Vinogradov 1937, Chen-Wang 1989)
"trade off" zwischen Größe der Konstanten und Qualität
der Aussagen.
Additive Zahlentheorie: Hardy-Littlewood, Gelfand-Linnik, Vinogradov, Brun, van der Corput, Schnirelman, Chen, Hua,...
Systematische Fragestellungen um Primzahlen
 ist
Primzahl
ist
Primzahl![]()
 ,
, ![]()
![]() -te Primzahl
(
-te Primzahl
(![]() )
)
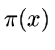 als Funktion von
als Funktion von  disjunkte
Zerlegung,
disjunkte
Zerlegung, Tabellen legen nahe:
![]()
C.F.Gauß (1777-1855)
A.M.Legendre (1752-1833)
 .
.
.
.
1792: 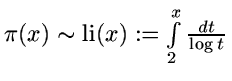 (?)
1808:
(?)
1808: 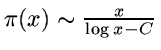 ,
, ![]() (?)
(?)
Dabei 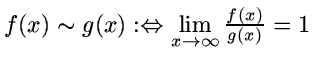
Leicht zu sehen:
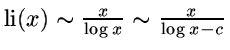 für
alle Konstanten
für
alle Konstanten ![]()
Deshalb sind beide Vermutungen äquivalent
("Primzahlsatz", bewiesen 1896 von
J. Hadamard (1865-1963) und C.J. de la Vallée Poussin (1866-1962)
)
 .
.
.
.
Folge: ![]()
| x | pi(x) | Gauß' Li | Legendre | x/(log x - 1) |
|---|---|---|---|---|
| 1000 | 168 | 178 | 172 | 169 |
| 10000 | 1229 | 1246 | 1231 | 1218 |
| 100000 | 9592 | 9630 | 9588 | 9512 |
| 1000000 | 78498 | 78628 | 78534 | 78030 |
| 10000000 | 664579 | 664918 | 665138 | 661459 |
| 100000000 | 5761455 | 5762209 | 5769341 | 5740304 |
| 1000000000 | 50847534 | 50849235 | 50917519 | 50701542 |
| 10000000000 | 455052511 | 455055614 | 455743004 | 454011971 |
Annäherungen
P.L. Chebyshev (1821-1894)

ca. 1850: es gibt Konstanten ![]() ,
, ![]() mit:
mit:
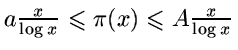 ,falls
,falls ![]() ,
,
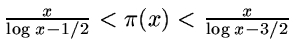
Weiter:
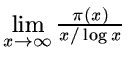 ,
so ist dieser
,
so ist dieser
Chebyshevs Resultate gleichzeitig schwächer (Natur der Konstanten ![]() )
und stärker (explizite Fehlerabschätzung) als der Primzahlsatz.
)
und stärker (explizite Fehlerabschätzung) als der Primzahlsatz.
Vermutung von Bertrand ![]() mit
mit ![]()
Verschärfung: Zwischen je zwei Quadratzahlen liegt mindestens eine Primzahl (?)
B.Riemann (1826-1866)

B. Riemann, "Über die Anzahl der Primzahlen unter einer gegebenen Grösse" 1859
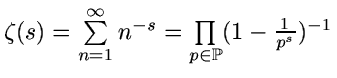
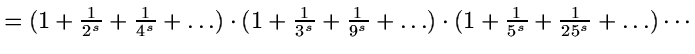 (Euler für
(Euler fürreell,
)
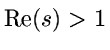
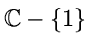 .
.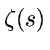 und
und 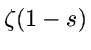 :
: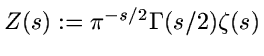 gilt
gilt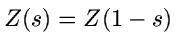
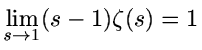
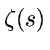 :
: 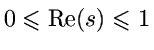 .
.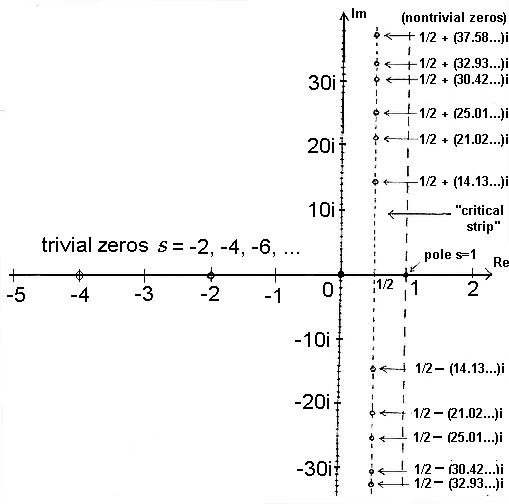
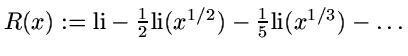
(ganze Funktion in ![]() ,
schnell konvergent, Gram 1893)
,
schnell konvergent, Gram 1893)
und:
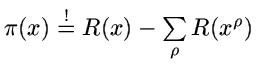 ,
,
wobei ![]() durch die Nullstellen von
durch die Nullstellen von 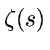 im kritischen Streifen läuft.
im kritischen Streifen läuft.
Fehlerabschätzung von 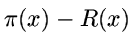
![]() Kenntnis der Nullstellen von
Kenntnis der Nullstellen von 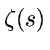
Der Absolutbetrag der Zeta-Funktion (Pol bei 0 sichtbar)
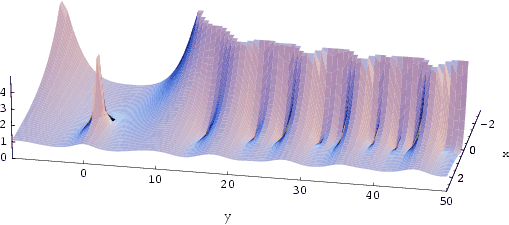
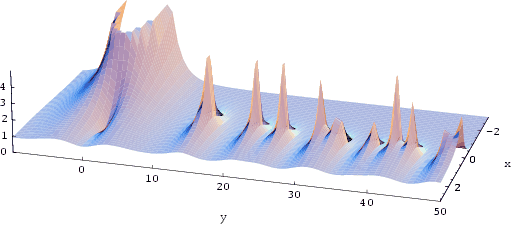
Vermutung von Riemann:
Die nichttrivialen Nullstellen von 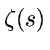 liegen alle auf der kritischen Geraden (?)
liegen alle auf der kritischen Geraden (?)
Konsequenzen:
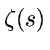 hat
keine Nullstellen mit
hat
keine Nullstellen mit 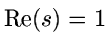 "
"(wurde bewiesen von Hadamard, de la Vallée Poussin 1896; starke Vereinfachung durch Newman 1980; Zahlentheoriebuch von H. Koch 1997)
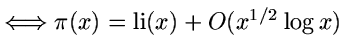 (Riemann
1859)
(Riemann
1859)
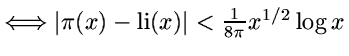 für
für 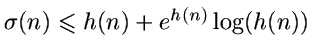 ,
,
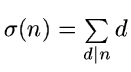 und
und 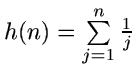 (Lagarias 2000)
(Lagarias 2000)Bekannte Aussagen in Richtung der Vermutung:
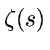 liegen auf der kritischen Geraden (Hardy 1914)
liegen auf der kritischen Geraden (Hardy 1914)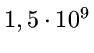 Nullstellen (geordnet nach Imaginärteil) liegen auf der kritischen
Geraden (Van de Lune, te Riele, Winter 1986)
Nullstellen (geordnet nach Imaginärteil) liegen auf der kritischen
Geraden (Van de Lune, te Riele, Winter 1986)
Statistik der Nullstellen![]() Statistik der Eigenwerte zufälliger hermitescher Matrizen (Vielteilchenphysik)
Statistik der Eigenwerte zufälliger hermitescher Matrizen (Vielteilchenphysik)
Riemanns Formel
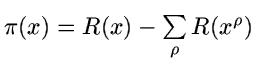
im Prinzip geeignet zur exakten Berechnung von 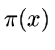 für große
für große ![]() .
Effektivere Methode (Meissel 1885, Lehmer, Lagaries, Miller, Odlyzko,...)
.
Effektivere Methode (Meissel 1885, Lehmer, Lagaries, Miller, Odlyzko,...)
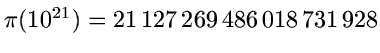
Andere Verteilungsprobleme:
3 7 11 15 19 23 27 31 35 39 43...
5 9 13 17 21 25 29 33 37 41 ...
Treten in beiden Folgen unendlich viele Primzahlen auf?
Verallgemeinerung: Sind ![]() teilerfremde ganze Zahlen,
teilerfremde ganze Zahlen, ![]() ,
gilt (Legendre 1808):
,
gilt (Legendre 1808):
"![]() enthält
unendlich viele Primzahlen." (?)
enthält
unendlich viele Primzahlen." (?)
G.L. Dirichlet (1805-1859)

1837-1840: Ja! Genauer:
Für 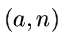 wie oben gilt:
wie oben gilt:
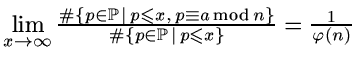
Dazu: Erfindung der "Dirichlet'schen L-Funktionen"
Beispiel: ![]()
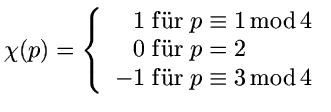
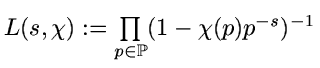
(Verallgemeinerung der Zeta-Funktion, holomorphe Fortsetzung vom Konvergenzgebiet
auf ganz ![]() )
)
Satz von Dirichlet folgt (für ![]() )
aus
)
aus 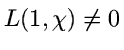 .
.
Es ist
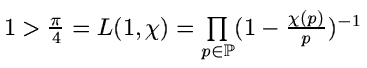
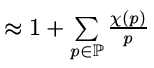
Dies macht plausibel: Trotz asymptotischer Äquivalenz auf endlichem
Niveau etwas mehr ![]() als
als ![]() .
.
| Bedingung | Anzahl <1000 | <2000 | <5000 | <10000 | <20000 | <50000 | <100000 |
| 80 | 147 | 329 | 609 | 1125 | 2549 | 4783 | |
| 87 | 155 | 339 | 619 | 1136 | 2583 | 4808 |
Quadratische statt lineare Progression:
Gibt es unendlich viele Primzahlen z.B. in  ?
?
(Vermutung von Hardy-Littlewood 1917)
Polynome höheren Grades?
Antwort unbekannt!
C.H. Cramér (1893-1985) G.H.
Hardy (1877-1947) J.E. Littlewood (1885-1977)
 .
.
.
. .
.
.
.
Ausgehend von der "Annahme":
"Eine große Zahl ![]() ist mit Wahrscheinlichkeit
ist mit Wahrscheinlichkeit 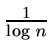 prim (unabhängig für alle
prim (unabhängig für alle ![]() )"
)"
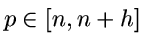 ,
, | Intervall | Primzahlen
erwartet gefunden |
Primzahlzwillinge
erwartet gefunden |
| 1 000 000 000-
1 000 150 000 |
7238 7242 | 461 466 |
| 100 000 000 000-
100 000 150 000 |
5922 5974 | 309 276 |
| 10 000 000 000 000-
10 000 000 150 000 |
5011 5065 | 211 208 |
| 1 000 000 000 000 000-
1 000 000 000 150 000 |
4343 4251 | 166 161 |
Nicht bekannt, ob es unendlich viele Primzahlzwillinge gibt! Aber (Brun 1919)
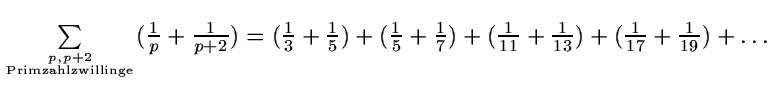
konvergent (gegen Wert ![]() )
)
Primzahlerzeugung
Gibt es eine einfache Funktion ![]() mit
mit 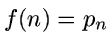 ?
?
Es ist 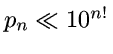 ,
also
,
also 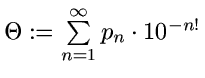 konvergent und
konvergent und
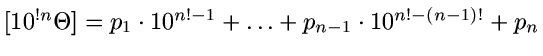
Tautologisch!
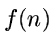 immer/oft prim?
immer/oft prim?Beispiel (Euler):.
Dann istprim für
,
.
Ebenso: Für,
hat
prime Werte für
.
Grund: Der imaginär-quadratische Körperhat für diese
die Klassenzahl 1 (Rabinowitsch 1912)
Aber: Jedes nichtkonstante Polynom mit Koeffizienten in(oder
) liefert bei Einsetzen von
unendlich viele nichtprime Werte (Übungsaufgabe).
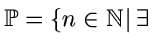 nichtnegative ganze Zahlen
nichtnegative ganze Zahlen 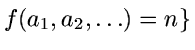
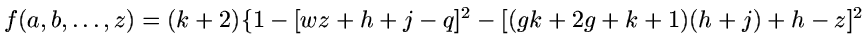
Primzahltests
"Dass die Aufgabe, die Primzahlen von den zusammengesetzten zu unterscheiden
und letztere in ihre Primfactoren zu zerlegen, zu den wichtigsten und nützlichsten
der gesamten Arithmetik gehört und die Bemühungen und den Scharfsinn
sowohl der alten wie auch der neueren Geometer in Anspruch genommen hat,
ist so bekannt, dass es überflüssig wäre, hierüber
viele Worte zu verlieren...ausserdem aber dürfte es die Würde
der Wissenschaft erheischen, alle Hülfsmittelzur Lösung jenes
so eleganten und berühmten Problems fleissig zu vervollkommnen"
(Gauß, Disquisitiones Arithmeticae, Abs. 329)
Rekorde
hat ![]() Stellen.
Stellen.
(GIMPS=Great Internet Mersenne Prime Search)
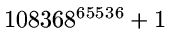
hat ![]() Stellen (
Stellen (![]() )
)
| Number | Digits | Year | Machine | Prover |
|---|---|---|---|---|
| 180(M127)2+1 | 79 | 1951 | EDSAC1 | Miller & Wheeler |
| M521 | 157 | 1952 | SWAC | Robinson (Jan 30) |
| M607 | 183 | 1952 | SWAC | Robinson (Jan 30) |
| M1279 | 386 | 1952 | SWAC | Robinson (June 25) |
| M2203 | 664 | 1952 | SWAC | Robinson (Oct 7) |
| M2281 | 687 | 1952 | SWAC | Robinson (Oct 9) |
| M3217 | 969 | 1957 | BESK | Riesel |
| M4423 | 1332 | 1961 | IBM7090 | Hurwitz |
| M9689 | 2917 | 1963 | ILLIAC 2 | Gillies |
| M9941 | 2993 | 1963 | ILLIAC 2 | Gillies |
| M11213 | 3376 | 1963 | ILLIAC 2 | Gillies |
| M19937 | 6002 | 1971 | IBM360/91 | Tuckerman |
| M21701 | 6533 | 1978 | Cyber 174 | Noll & Nickel |
| M23209 | 6987 | 1979 | Cyber 174 | Noll |
| M44497 | 13395 | 1979 | Cray 1 | Nelson & Slowinski |
| M86243 | 25962 | 1982 | Cray 1 | Slowinski |
| M132049 | 39751 | 1983 | Cray X-MP | Slowinski |
| M216091 | 65050 | 1985 | Cray X-MP | Slowinski |
| 391581*2216193-1 | 65087 | 1989 | Amdahl 1200 | Amdahl Six |
| M756839 | 227832 | 1992 | Cray-2 | Slowinski & Gage |
| M859433 | 258716 | 1994 | Cray C90 | Slowinski & Gage |
| M1257787 | 378632 | 1996 | Cray T94 | Slowinski & Gage |
| M1398269 | 420921 | 1996 | Pentium (90 Mhz) | Armengaud, Woltman, et. al. [GIMPS] |
| M2976221 | 895932 | 1997 | Pentium (100 Mhz) | Spence, Woltman, et. al. [GIMPS] |
| M3021377 | 909526 | 1998 | Pentium (200 Mhz) | Clarkson, Woltman, Kurowski, et. al. [GIMPS, PrimeNet] |
| M6972593 | 2098960 | 1999 | Pentium (350 Mhz) | Hajratwala, Woltman, Kurowski, et. al. [GIMPS, PrimeNet] |
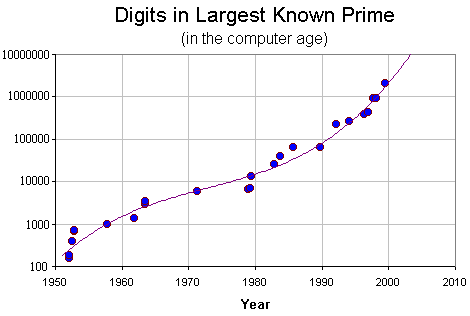
Eine kubische Extrapolation dieser Daten würde folgenden Entdeckungen vorhersagen:
- eine 10 000 000-stellige Primzahl Ende 2001
- eine 100 000 000-stellige Primzahl Mitte 2004
- eine 1 000 000 000-stellige Primzahl Anfang 2006
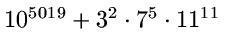
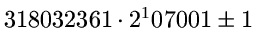
habenStellen
(die erste der Länge ![]() )
)
Weitere der Länge ![]() bei
bei ![]()
bei
bei