




Next: Der adjungierte Operator
Up: Der Dual
Previous: Der Dual
Daraus ergeben sich die folgenden Formeln: Sind X und Ymatrixnormierte Räume,
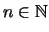 ,
,
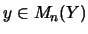 und
und
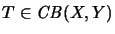 ,
so ist
,
so ist
und
Eine Matrix
![$[T_{ij}]\in M_n(X^*)$](img89.gif) definiert einen Operator
definiert einen Operator
Dadurch ist eine algebraische Identifizierung von Mn(X*) mit Mn(X)* und
weiter von
Mn(X**) mit
Mn(X)** gegeben. Letztere stellt sich sogar als
vollständige Isometrie heraus ([Ble92b, Cor. 2.14], für die Isometrie auf der
Grundstufe vgl. [Ble92a, Thm. 2.5]10):
Daraus folgt11
X heißt reflexiv,
falls
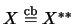 ist. Ein
Operatorraum X ist genau
dann reflexiv, falls seine erste Stufe M1(X) als Banachraum reflexiv ist.
ist. Ein
Operatorraum X ist genau
dann reflexiv, falls seine erste Stufe M1(X) als Banachraum reflexiv ist.
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() definiert einen Operator
definiert einen Operator
![\begin{eqnarray*}T:M_n(X)&\to&{\mathbb{C} }\\
\left[x_{ij}\right]&\mapsto&\sum_{i,j}T_{ij}x_{ij}
\mbox{.}
\end{eqnarray*}](img90.gif)
![]() ist. Ein
Operatorraum X ist genau
dann reflexiv, falls seine erste Stufe M1(X) als Banachraum reflexiv ist.
ist. Ein
Operatorraum X ist genau
dann reflexiv, falls seine erste Stufe M1(X) als Banachraum reflexiv ist.