




Next: Multiplikative Strukturen
Up: Hilbertsche Operatorräume
Previous: Charakterisierungen
Seien X, Y Operatorräume. Wir sagen, eine lineare Abbildung
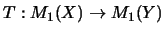 faktorisiere durch einen
Spalten-Hilbertraum ,
wenn es einen Hilbertraum
faktorisiere durch einen
Spalten-Hilbertraum ,
wenn es einen Hilbertraum
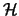 und vollständig beschränkte Abbildungen
und vollständig beschränkte Abbildungen
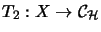 ,
,
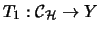 gibt mit
gibt mit
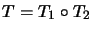 .
Wir definieren
.
Wir definieren
wobei das Infimum über alle Faktorisierungen gebildet wird, und
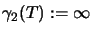 ,
falls keine solche Faktorisierung existiert.
,
falls keine solche Faktorisierung existiert.
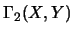 bezeichne den Banachraum aller linearen Abbildungen
bezeichne den Banachraum aller linearen Abbildungen
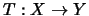 mit
mit
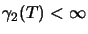 [ER91, Chap. 5],[Ble92b, p. 83].
[ER91, Chap. 5],[Ble92b, p. 83].
Seien noch X1, Y1 Operatorräume und
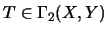 ,
,
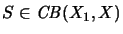 ,
,
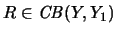 ,
so gilt die
,
so gilt die
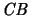 -Idealeigenschaft
-Idealeigenschaft
Eine Matrix
![$T=[T_{ij}] \in M_n(\Gamma_2(X,Y))$](img200.gif) wird als Abbildung von X nach
Mn(Y) gelesen:
[Tij](x):=[Tij(x)]. T besitzt eine Faktorisierung
in vollständig beschränkte Abbildungen
wird als Abbildung von X nach
Mn(Y) gelesen:
[Tij](x):=[Tij(x)]. T besitzt eine Faktorisierung
in vollständig beschränkte Abbildungen
Wir definieren wieder
wobei das Infimum über alle Faktorisierungen gebildet wird,
und erhalten so eine Operatorraumstruktur auf
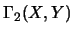 [ER91, Cor. 5.4].
[ER91, Cor. 5.4].
Seien X, Y Operatorräume und Y0 ein
Operatorunterraum von Y.
Dann ist die Einbettung
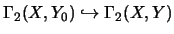 vollständig isometrisch [ER91, Prop. 5.2].
vollständig isometrisch [ER91, Prop. 5.2].
Seien X, Y Operatorräume. Bekanntlich definiert jede lineare Abbildung
ein lineares Funktional
über
Über diese Identifikation erhalten wir die vollständige Isometrie
[ER91, Thm. 5.3] [Ble92b, Thm. 2.11]
Seien X, Y, Z Operatorräume. Wir erhalten
eine vollständige Isometrie
über die Abbildung
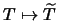 ,
gemäß
,
gemäß
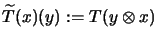 [ER91, Cor. 5.5].
[ER91, Cor. 5.5].





Next: Multiplikative Strukturen
Up: Hilbertsche Operatorräume
Previous: Charakterisierungen
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() ,
,
![]() ,
,
![]() ,
so gilt die
,
so gilt die
![]() -Idealeigenschaft
-Idealeigenschaft
![]() wird als Abbildung von X nach
Mn(Y) gelesen:
[Tij](x):=[Tij(x)]. T besitzt eine Faktorisierung
in vollständig beschränkte Abbildungen
wird als Abbildung von X nach
Mn(Y) gelesen:
[Tij](x):=[Tij(x)]. T besitzt eine Faktorisierung
in vollständig beschränkte Abbildungen
![]() vollständig isometrisch [ER91, Prop. 5.2].
vollständig isometrisch [ER91, Prop. 5.2].