Mit den nachstehenden Operatorraum-Strukturen ist ![]() vollständig isometrisch isomorph
zu einer Operatoralgebra:
vollständig isometrisch isomorph
zu einer Operatoralgebra:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Allgemein ist der Raum ![]() vollständig isometrisch isomorph zu einer Operatoralgebra,
wenn man ihn mit einer Operatorraum-Struktur
versieht, die sowohl
vollständig isometrisch isomorph zu einer Operatoralgebra,
wenn man ihn mit einer Operatorraum-Struktur
versieht, die sowohl
![]() als auch
als auch
![]() dominiert .
dominiert .
Mit den nachstehenden Operatorraum-Strukturen ist ![]() nicht vollständig isomorph zu einer Operatoralgebra:
nicht vollständig isomorph zu einer Operatoralgebra:
![]() ,
,
![]() .
.
Allgemein ist der Raum ![]() nicht vollständig isomorph zu einer Operatoralgebra,
wenn er eine Operatorraum-Struktur
trägt, die sowohl von
nicht vollständig isomorph zu einer Operatoralgebra,
wenn er eine Operatorraum-Struktur
trägt, die sowohl von
![]() als auch von
als auch von
![]() dominiert wird.
dominiert wird.
In den Randfällen p=1 resp.
- (a)
- Mit jeder beliebigen Operatorraum-Struktur ist
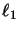 vollständig isometrisch isomorph zu einer Operatoralgebra.
vollständig isometrisch isomorph zu einer Operatoralgebra.
- (b)
-
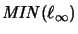 ist bis auf vollständige Isomorphie die einzige Operatoralgebra-Struktur auf
ist bis auf vollständige Isomorphie die einzige Operatoralgebra-Struktur auf
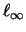 .
.
- (a)
-
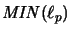 ist vollständig isomorph zu einer Operatoralgebra genau dann, wenn p=1 oder
ist vollständig isomorph zu einer Operatoralgebra genau dann, wenn p=1 oder 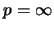 .
.
- (b)
-
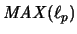 ist im Falle
ist im Falle
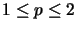 vollständig
isometrisch isomorph zu einer Operatoralgebra.
Sonst ist
vollständig
isometrisch isomorph zu einer Operatoralgebra.
Sonst ist
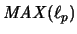 nicht vollständig isomorph zu einer Operatoralgebra.
nicht vollständig isomorph zu einer Operatoralgebra.
Für jedes
Wir schreiben OSp für die Operatorraum-Struktur, die G. Pisier auf Sp eingeführt hat. Man erhält diese
Operatorraum-Struktur durch komplexe Interpolation zwischen
![]() und
und
![]() .
.
- (a)
- Betrachten wir zunächst das gewöhnliche Produkt auf den Schatten-Klassen Sp.
Hierfür ergibt sich das nachstehende negative
Resultat [BLM95, Thm. 6.3]:
Für kein
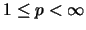 ist der Operatorraum OSp mit dem gewöhnlichen Produkt vollständig isomorph
zu einer Operatoralgebra.
ist der Operatorraum OSp mit dem gewöhnlichen Produkt vollständig isomorph
zu einer Operatoralgebra.
- (b)
- Betrachten wir nun das Schur-Produkt auf den Schatten-Klassen Sp.
Hiermit sind, sogar für verschiedene Operatorraum-Strukturen,
positive Ergebnisse möglich:
- (b1)
-
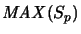 mit dem Schur-Produkt ist im Falle
mit dem Schur-Produkt ist im Falle
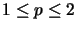 vollständig isometrisch isomorph
zu einer Operatoralgebra [BLM95, Thm. 6.1].
vollständig isometrisch isomorph
zu einer Operatoralgebra [BLM95, Thm. 6.1].
- (b2)
- OSp mit dem Schur-Produkt ist im Falle
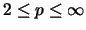 vollständig isometrisch isomorph
zu einer Operatoralgebra [BLM95, Cor. 6.4].
vollständig isometrisch isomorph
zu einer Operatoralgebra [BLM95, Cor. 6.4].