




Next: Duales Operatorraum-Tensorprodukt
Up: Tensorprodukte
Previous: Tensorprodukte
Operatorraum-Tensorprodukte
Ein Operatorraum-Tensorprodukt entsteht durch Vervollständigung des
algebraischen Tensorproduktes bezüglich einer
Operatorraum-Tensornorm.
Eine
Operatorraum-Tensornorm
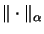 versieht für jedes Paar (X,Y) von Operatorräumen das algebraische Tensorprodukt
versieht für jedes Paar (X,Y) von Operatorräumen das algebraische Tensorprodukt
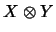 mit der Struktur eines
matrixnormierten Raumes ,
so daß die nachstehenden zwei Eigenschaften gelten
[BP91, Def. 5.9].
mit der Struktur eines
matrixnormierten Raumes ,
so daß die nachstehenden zwei Eigenschaften gelten
[BP91, Def. 5.9].
Der durch Vervollständigung entstehende Operatorraum
heißt
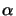 - Operatorraum-Tensorprodukt
von X und Y und wird mit
- Operatorraum-Tensorprodukt
von X und Y und wird mit
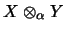 bezeichnet.
bezeichnet.
- 1.
- Für die komplexen Zahlen gilt
- 2.
-
Für alle
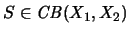 und
und
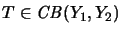 hat der Operator
hat der Operator
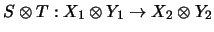 eine stetige Fortsetzung
eine stetige Fortsetzung
Die bilineare Abbildung
ist
allgemein vollständig kontrahierend .
22
-
- Man
kann die Forderung
2 durch die Forderungen
3 und
4 ersetzen.23
- 3.
-
Ein Operatorraum-Tensorprodukt
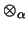 ist funktoriell:
Für alle
ist funktoriell:
Für alle
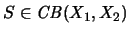 und
und
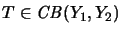 hat der Operator
hat der Operator
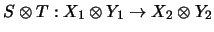 eine stetige Fortsetzung
eine stetige Fortsetzung
und es gilt
-
- Anmerkung: Dann
gilt sogar
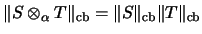 .
.
- 4.
-
Der algebraische
shuffle -Isomorphismus
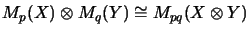 hat eine stetige Fortsetzung
hat eine stetige Fortsetzung
Diese
shuffle -Abbildung des
Operatorraum-Tensorproduktes ist vollständig kontrahierend.
Äquivalent zu 4 ist, daß die beiden
shuffle-Abbildungen
vollständig kontrahierend sind.
Operatorraum-Tensorprodukte
können noch weitere spezielle Eigenschaften haben:
Ein Operatorraum-Tensorprodukt
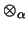 heißt
heißt
-
-
symmetrisch,
wenn
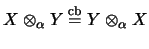 eine vollständige Isometrie ist;
eine vollständige Isometrie ist;
-
-
assoziativ,
wenn
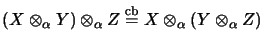 eine vollständige Isometrie ist;
eine vollständige Isometrie ist;
-
-
injektiv,
wenn für alle Unterräume
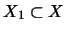 ,
,
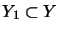 die
Abbildung
die
Abbildung
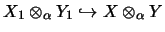 eine vollständige Isometrie ist;
eine vollständige Isometrie ist;
-
-
projektiv,
wenn für alle Unterräume
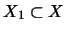 ,
,
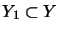 die
Abbildung
die
Abbildung
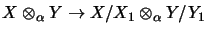 eine vollständige Quotientenabbildung ist;
eine vollständige Quotientenabbildung ist;
-
-
selbstdual,
wenn die algebraische
Einbettung
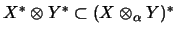 eine vollständige isometrische Fortsetzung
eine vollständige isometrische Fortsetzung
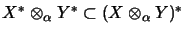 hat.
hat.
In vielen Anwendungen tritt die
Haagerup -Tensorprodukt auf.
Es ist nicht symmetrisch, aber assoziativ, injektiv,
projektiv
und selbstdual.





Next: Duales Operatorraum-Tensorprodukt
Up: Tensorprodukte
Previous: Tensorprodukte
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() versieht für jedes Paar (X,Y) von Operatorräumen das algebraische Tensorprodukt
versieht für jedes Paar (X,Y) von Operatorräumen das algebraische Tensorprodukt
![]() mit der Struktur eines
matrixnormierten Raumes ,
so daß die nachstehenden zwei Eigenschaften gelten
[BP91, Def. 5.9].
mit der Struktur eines
matrixnormierten Raumes ,
so daß die nachstehenden zwei Eigenschaften gelten
[BP91, Def. 5.9].
![]() - Operatorraum-Tensorprodukt
von X und Y und wird mit
- Operatorraum-Tensorprodukt
von X und Y und wird mit
![]() bezeichnet.
bezeichnet.
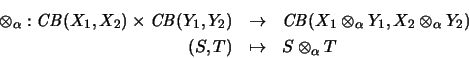
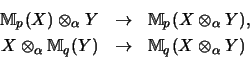
![]() heißt
heißt