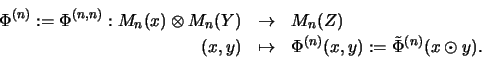Amplifikation

   

In der Literatur werden zwei unterschiedliche Definitionen der  Amplifikation einer bilinearen Abbildung gebraucht.

Wir bezeichnen die erste Art 1 der Amplifikation als allgemeine Amplifikation. Diese allgemeine Amplifikation verwendet man, um aus einer einer Dualität $\langle X, X^ * \rangle$ eine Matrix-Dualität zu bilden, die der Dualitätstheorie der Operatorräume zugrundeliegt. Die allgemeine Amplifikation führt auf den Begriff der allgemein vollständig beschränkten bilinearen Abbildungen und auf das projektive Operatoraum-Tensorprodukt.

Die zweite Art   2 der Amplifikation nennen wir die Amplifikation einer bilinearen Abbildung. Diese Amplifikation führt auf den Begriff der vollständig beschränkten bilinearen Abbildungen und auf das Haagerup Tensorprodukt. Wir verwenden im folgenden die Symbole $\Phi: X \times Y \rightarrow Z$ für eine bilineare Abbildung und $\tilde\Phi : X \otimes Y \rightarrow Z$ für ihre Linearsierung.  

Die beiden Definitionen der Amplifikationen einer bilinearen Abbildung $\Phi$ erfolgen mit Hilfe der Amplifikation ihrer Linearisierung:

$$\tilde\Phi^{(n)} : M_{n}(X \otimes Y) \rightarrow M_{n}(Z).$$

1.

  Die allgemeine Amplifikation von $\Phi$ ergibt die bilineare Abbildung  

$$\Phi^{(p \times q)} : (x, y) \mapsto \tilde\Phi^{(pq)}(x \otimes y) = [\Phi(x_{ij},y_{kl})] \in M_p(M_q(Z)) = M_{pq}(Z).$$

der Operatormatrizen $x = [x_{ij}] \in M_{p}(X)$, $y = [y_{kl}] \in M_{q}(Y)$. Dabei ist das Tensorprodukt der Operatormatrizen erklärt als

$$x \otimes y = [x_{ij}] \otimes [y_{kl}] := [ x_{ij} \otimes y_{kl} ] \in M_{pq}(X \otimes Y) = M_p(M_q(X \otimes Y)).$$

2.

   Im Zusammenhang mit vollständig beschränkten bilinearen Abbildungen verwendet man die  tensorielle Matrixmultiplikation [Eff87]

$$\mbox{$ x \odot y = [x_{ij}] \odot [y_{jk}] := \left[\su... ...1}^l x_{ij} \otimes y_{jk}\right] \in M_{n}(X \otimes Y) $ }$$

von Operatormatrizen $x = [x_{ij}] \in M_{n,l}(X)$, $y = [y_{jk}]\in M_{l,n}(Y)$.

Weitere Formeln findet man im Abschnitt tensorielle Matrixmultiplikation .

Die (n,l)-te  Amplifikation     einer bilinearen Abbildung $\Phi: X \times Y \rightarrow Z$ wird definiert als

$$\begin{eqnarray*}\Phi^{(n,l)} : M_{n,l}(X) \times M_{l,n}(Y) &\rightarrow& M_... ...box{$\sum_{j=1}^l \Phi(x_{ij}, y_{jk})$ } \right] \in M_{n}(Z) \end{eqnarray*}$$

für $l,n \in {\mathbb{N} }$, $x = [x_{ij}] \in M_{n,l}(X)$, $y = [y_{jk}]\in M_{l,n}(Y)$. Wenn n=l, schreiben wir kurz³⁸

$$\begin{eqnarray*}\Phi^{(n)} := \Phi^{(n,n)}: M_n(x) \otimes M_n(Y) &\rightarrow... ...(x,y) &\mapsto& \Phi^{(n)}(x,y) := \tilde\Phi^{(n)}(x \odot y). \end{eqnarray*}$$