




Next: Modul-Tensorprodukte
Up: Vollständig beschränkte bilineare Abbildungen
Previous: Vollständige Beschränktheit
Darstellung
Vollständig
beschränkte Bilinearformen wurden zuerst auf C*-Algebren
A, B untersucht
[EK87].
Für eine Bilinearform
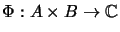 sind die folgenden Eigenschaften äquivalent:
sind die folgenden Eigenschaften äquivalent:
- (1)
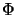 ist vollständig beschränkt.
ist vollständig beschränkt.
- (2)
- Es gibt eine Konstante c, so daß
für alle
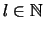 ,
,
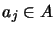 ,
,
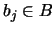 gilt.
gilt.
- (3)
- Es gibt eine Konstante c und Zustände
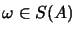 ,
,
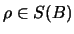 ,
so daß
,
so daß
für alle 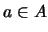 ,
,
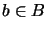 gilt.
gilt.
- (4)
- Es gibt *-Darstellungen
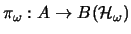 und
und
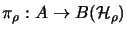 mit zyklischen Vektoren
mit zyklischen Vektoren
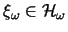 ,
,
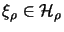 und einen Operator
und einen Operator
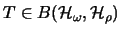 ,
so daß
,
so daß
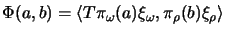 für alle
für alle 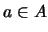 ,
,
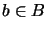 gilt.
gilt.
Man kann
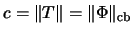 und
und
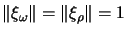 wählen.
42
wählen.
42
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() sind die folgenden Eigenschaften äquivalent:
sind die folgenden Eigenschaften äquivalent: