




Next: Charakterisierungen von Hilbert-C*-Moduln
Up: Hilbert-C*-Moduln
Previous: Das äußere Tensorprodukt von Hilbert-C*-Moduln
Es seien X und Y rechte Hilbert-C*-Moduln über einer
C*-Algebra A.
Es bezeichne
B(X,Y)A
den Raum der linearen, beschränkten Rechts-A-Modulhomomorphismen
von X nach Y,
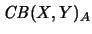 den Raum der Abbildungen aus B(X,Y)A, die zusätzlich vollständig
beschränkt sind. Es gilt isometrisch isomorph:
den Raum der Abbildungen aus B(X,Y)A, die zusätzlich vollständig
beschränkt sind. Es gilt isometrisch isomorph:
Das heißt: Jeder beschränkte A-Rechts-Modulhomomorphismus T ist
vollständig beschränkt, und es gilt:
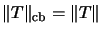 [Ble97].
Zusätzlich gilt [Pas73]:
[Ble97].
Zusätzlich gilt [Pas73]:
Ein Operator
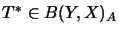 heißt
adjungierter Operator
zu einem Operator
heißt
adjungierter Operator
zu einem Operator
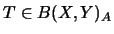 ,
wenn für alle
,
wenn für alle 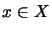 und
und 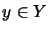 gilt:
gilt:
Existiert zu T ein solches T*, so heißt T adjungierbar.
Nicht jeder Operator
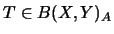 ist adjungierbar.
ist adjungierbar.
Die Menge der adjungierbaren Operatoren
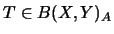 wird im
folgenden mit
Bad(X,Y) bezeichnet.
Bad(X) ist eine C*-Algebra.
wird im
folgenden mit
Bad(X,Y) bezeichnet.
Bad(X) ist eine C*-Algebra.
Ein Operator der Form
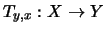 ,
,
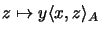 heißt elementarer Operator.
Ein wichtiger Unterraum von
Bad(X,Y) ist
K(X,Y),
die abgeschlossene lineare Hülle aller elementaren Operatoren,
abgeschlossen bzgl. der von
heißt elementarer Operator.
Ein wichtiger Unterraum von
Bad(X,Y) ist
K(X,Y),
die abgeschlossene lineare Hülle aller elementaren Operatoren,
abgeschlossen bzgl. der von
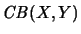 induzierten Norm.
Die Operatorraumstruktur, die
K(X) als Teilmenge von
induzierten Norm.
Die Operatorraumstruktur, die
K(X) als Teilmenge von
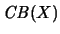 erbt,
entspricht der Operatorraumstruktur, die
K(X) in kanonischer Weise
als C*-Algebra trägt.
Es gilt
erbt,
entspricht der Operatorraumstruktur, die
K(X) in kanonischer Weise
als C*-Algebra trägt.
Es gilt
vollständig isometrisch via
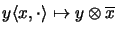 [Ble97].
[Ble97].





Next: Charakterisierungen von Hilbert-C*-Moduln
Up: Hilbert-C*-Moduln
Previous: Das äußere Tensorprodukt von Hilbert-C*-Moduln
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() wird im
folgenden mit
Bad(X,Y) bezeichnet.
Bad(X) ist eine C*-Algebra.
wird im
folgenden mit
Bad(X,Y) bezeichnet.
Bad(X) ist eine C*-Algebra.
![]() ,
,
![]() heißt elementarer Operator.
Ein wichtiger Unterraum von
Bad(X,Y) ist
K(X,Y),
die abgeschlossene lineare Hülle aller elementaren Operatoren,
abgeschlossen bzgl. der von
heißt elementarer Operator.
Ein wichtiger Unterraum von
Bad(X,Y) ist
K(X,Y),
die abgeschlossene lineare Hülle aller elementaren Operatoren,
abgeschlossen bzgl. der von
![]() induzierten Norm.
Die Operatorraumstruktur, die
K(X) als Teilmenge von
induzierten Norm.
Die Operatorraumstruktur, die
K(X) als Teilmenge von
![]() erbt,
entspricht der Operatorraumstruktur, die
K(X) in kanonischer Weise
als C*-Algebra trägt.
Es gilt
erbt,
entspricht der Operatorraumstruktur, die
K(X) in kanonischer Weise
als C*-Algebra trägt.
Es gilt