




Next: Interpolation
Up: Interpolation
Previous: Interpolation
Seien X und Y Operatorräume, so daß M1(X) und M1(Y) eingebettet sind in einen Hausdorffschen topologischen Vektorraum.
Dann normieren wir
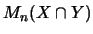 gemäß
gemäß
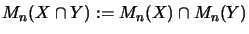 ,
also
,
also
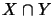 heißt
Operatorraumschnitt.
heißt
Operatorraumschnitt.
Für Operatorräume62
X, Y betten wir
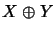 in
in
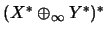 ein und erhalten so
eine Operatorraumstruktur
ein und erhalten so
eine Operatorraumstruktur
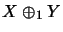 .
Sei
.
Sei
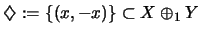 .
Die Quotienten-Operatorraumstruktur
.
Die Quotienten-Operatorraumstruktur
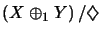 heißt
Operatorraumsumme und wird mit X+Y bezeichnet.
Wir haben also
heißt
Operatorraumsumme und wird mit X+Y bezeichnet.
Wir haben also
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04