



Next: The adjoint operator
Up: The dual
Previous: The dual
Contents
Index
For matricially normed spaces 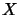 and
and 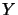 ,
,
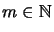 ,
,
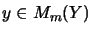 and
and
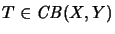 we have
and
we have
and
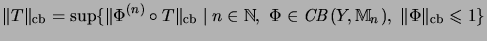
.
A matrix
![$ [T_{ij}]\in M_n(X^*)$](img137.png) defines an operator
defines an operator
Thus we have an algebraic identification of 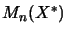 and
and 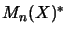 and
further of
and
further of
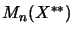 and
and
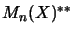 . The latter even is a complete isometry
([Ble92b, Cor. 2.14]):
. The latter even is a complete isometry
([Ble92b, Cor. 2.14]):
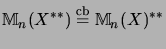
.
The isometry on the first matrix level is shown in [Ble92a, Thm. 2.5]. This
already implies11the complete isometry.
More generally we have12
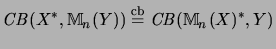
.
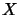 is called reflexive,
if
is called reflexive,
if
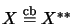 . An
operator space
. An
operator space 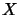 is reflexive if and only if its first matrix level
is reflexive if and only if its first matrix level
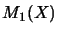 is a reflexive Banach space.
is a reflexive Banach space.
Footnotes
- ... implies11
-
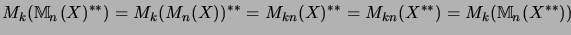
.
- ... have12
-
This follows from
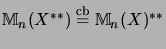 and the above mentioned formula
and the above mentioned formula
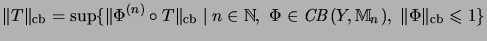
.




Next: The adjoint operator
Up: The dual
Previous: The dual
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() defines an operator
defines an operator
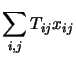 .
.![]() is called reflexive,
if
is called reflexive,
if
![]() . An
operator space
. An
operator space ![]() is reflexive if and only if its first matrix level
is reflexive if and only if its first matrix level
![]() is a reflexive Banach space.
is a reflexive Banach space.