



Next: Direct sums
Up: The dual
Previous: Some formulae
Contents
Index
For
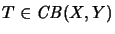 , the
adjoint operator
, the
adjoint operator 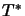 is defined as usual.
We have:
is defined as usual.
We have:
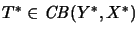 , and
, and
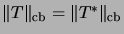 .
The mapping
.
The mapping
even is completely isometric [Ble92b, Lemma 1.1].13
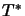 is a
complete quotient mapping if and only if
is a
complete quotient mapping if and only if 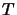 is completely isometric;
is completely isometric; 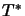 is completely isometric if
is completely isometric if 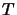 is a complete
quotient mapping. Especially for a subspace
is a complete
quotient mapping. Especially for a subspace
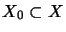 we have [Ble92a]:
we have [Ble92a]:
and, if 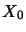 is closed,
is closed,
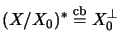
.
Footnotes
- ...Blecher92a.13
-
The isometry on the matrix levels follows from the isometry on the first matrix level
using the above mentioned formula
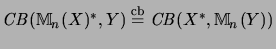 :
:




Next: Direct sums
Up: The dual
Previous: Some formulae
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() is a
complete quotient mapping if and only if
is a
complete quotient mapping if and only if ![]() is completely isometric;
is completely isometric; ![]() is completely isometric if
is completely isometric if ![]() is a complete
quotient mapping. Especially for a subspace
is a complete
quotient mapping. Especially for a subspace
![]() we have [Ble92a]:
we have [Ble92a]: