- Let
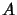 and
and 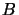 be C
be C -algebras in
-algebras in 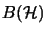 .
Then on the algebraic tensor product
.
Then on the algebraic tensor product
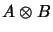 the Haagerup tensor norm is explicitly given by
where
the Haagerup tensor norm is explicitly given by
where
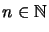 ,
,
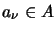 ,
,
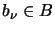 .
.
The Haagerup norm of
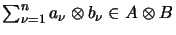 equals the
cb-norm of the elementary operator
equals the
cb-norm of the elementary operator
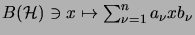 .
The Haagerup tensor product
.
The Haagerup tensor product
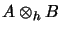 is the completion of the
algebraic tensor product
is the completion of the
algebraic tensor product
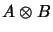 with respect to the above norm.
The following more general definition in particular
yields a completely isometric embedding
with respect to the above norm.
The following more general definition in particular
yields a completely isometric embedding
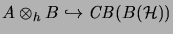 .
.
-
We
have
where
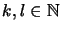 ,
,
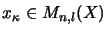 ,
,
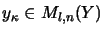 .
In fact, one summand suffices
[BP91, Lemma 3.2].
.
In fact, one summand suffices
[BP91, Lemma 3.2].
-
For
elements
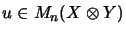 in the algebraic tensor product there is an
in the algebraic tensor product there is an
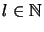 and elements
and elements
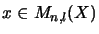 ,
,
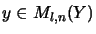 such that
such that
The infimum occuring in the formula describing the norm in this case is actually a minimum
[ER91, Prop. 3.5].
-
The
Haagerup norm of an element
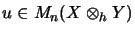 can also be expressed using a supremum:40
where
can also be expressed using a supremum:40
where
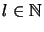 ,
,
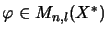 ,
,
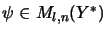 ,
,
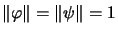 [ER91, Prop. 3.4].
[ER91, Prop. 3.4].
-
From
the definition of the Haagerup norm one easily deduces that the
shuffle -map
is a complete contraction.
Hence the Haagerup tensor product enjoys property
![[*]](crossref.png) of an operator space tensor product.
of an operator space tensor product.
But the shuffle-map is not an isometry in general
as shown by the following example:41
Since the bilinear mapping
is contractive, it is
jointly completely
contractive.42
In fact, using
![[*]](crossref.png) , we see that it is even
completely
contractive.
, we see that it is even
completely
contractive.
-
For
the row and column structure the
shuffle -map even is
a complete isometry.
We have the Lemma of Blecher and Paulsen
[BP91, Prop. 3.5]:
In many cases it suffices to prove a statement about the
Haagerup tensor product
on the first matrix level and then to deduce it for all matrix levels
using the above formula.43
Here we list some special cases of the Lemma of Blecher and Paulsen:
-
In
contrast to
![[*]](crossref.png) , for
, for
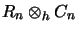 one obtains the finer operator space structure
of the trace class
one obtains the finer operator space structure
of the trace class
.
For an operator space  we have
[Ble92b, Prop. 2.3]:
we have
[Ble92b, Prop. 2.3]:
-
By
the very construction the bilinear mapping
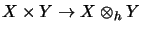 ,
,
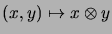 is a complete contraction.
is a complete contraction.
Hence its amplification,
the
tensor matrix product
also is a
complete contraction .
The linearization of the tensor matrix product gives the
complete contraction
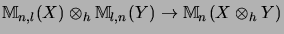
.

- The
bilinear mapping44
is
completely contractive 45and gives rise to a complete contraction
-
Let
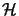 and
and
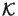 be Hilbert spaces.
Taking the Haagerup tensor product of the
column Hilbert space
be Hilbert spaces.
Taking the Haagerup tensor product of the
column Hilbert space
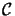 and the
row Hilbert space
and the
row Hilbert space
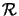 one obtains completely isometrically
the space of
compact operators
one obtains completely isometrically
the space of
compact operators 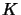 resp. of trace class46operators
resp. of trace class46operators 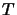 [ER91, Cor. 4.4]:
[ER91, Cor. 4.4]:
This
example
also shows that the Haagerup tensor product is not symmetric.
![]() equals the
cb-norm of the elementary operator
equals the
cb-norm of the elementary operator
![]() .
The Haagerup tensor product
.
The Haagerup tensor product
![]() is the completion of the
algebraic tensor product
is the completion of the
algebraic tensor product
![]() with respect to the above norm.
The following more general definition in particular
yields a completely isometric embedding
with respect to the above norm.
The following more general definition in particular
yields a completely isometric embedding
![]() .
.
![[*]](crossref.png) of an operator space tensor product.
of an operator space tensor product.
![[*]](crossref.png) , we see that it is even
completely
contractive.
, we see that it is even
completely
contractive.
![[*]](crossref.png) , for
, for
![$\displaystyle (\varphi \odot \psi)(x \otimes y)=
\langle x \otimes y, \varphi \...
...y , \varphi_{ij} \otimes \psi_{jk} \rangle\right]
= \varphi(x)\psi(y)
\in M_n.
$](img816.png)