



Next: -extreme points
Up: -convexity
Previous: -convexity
Contents
Index
Suppose that
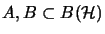 are unital
are unital 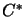 -algebras and
-algebras and
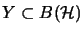 is a
is a 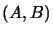 -bimodul. Then
-bimodul. Then
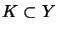 is
is 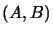 -absolutely convex, if
-absolutely convex, if
for all 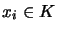 and
and 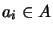 ,
, 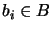 such that
such that
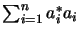 ,
,
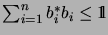 .
Let
.
Let 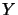 be a
be a 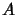 -bimodul. Then
-bimodul. Then 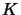 is
is 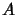 -convex, if
for all
-convex, if
for all 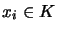 and
and 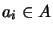 such that
such that
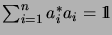 .
In the case
.
In the case 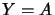 this definition is equivalent to the definition of
this definition is equivalent to the definition of 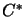 -convex sets.
-convex sets.
There are following separation theorems: Let
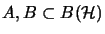 be unital
be unital 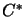 -algebras and
-algebras and
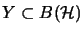 a
a 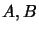 -bimodul. Let
-bimodul. Let
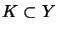 be norm closed and
be norm closed and
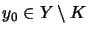 .
.
1) If 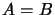 ,
, 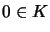 and
and 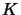 is
is 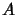 -convex, then there is a Hilbert space
-convex, then there is a Hilbert space 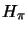 , a cyclic representation
, a cyclic representation
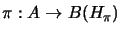 and a completely bounded
and a completely bounded 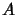 -bimodul-homomorphism, such that for all
-bimodul-homomorphism, such that for all 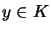
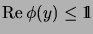
, but
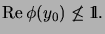
2)If 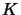 is
is 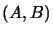 -absolutely convex, then there is a Hilbert space
-absolutely convex, then there is a Hilbert space 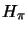 , representations
, representations
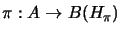 and
and
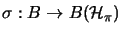 and a completely bounded
and a completely bounded 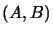 -bimodul-homomorphism
-bimodul-homomorphism
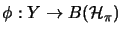 , such that for all
, such that for all 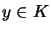
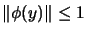
, but
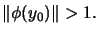
Prof. Gerd Wittstock
2001-01-07
![]() are unital
are unital ![]() -algebras and
-algebras and
![]() is a
is a ![]() -bimodul. Then
-bimodul. Then
![]() is
is ![]() -absolutely convex, if
-absolutely convex, if
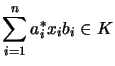
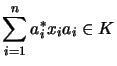
![]() be unital
be unital ![]() -algebras and
-algebras and
![]() a
a ![]() -bimodul. Let
-bimodul. Let
![]() be norm closed and
be norm closed and
![]() .
.
![]() ,
, ![]() and
and ![]() is
is ![]() -convex, then there is a Hilbert space
-convex, then there is a Hilbert space ![]() , a cyclic representation
, a cyclic representation
![]() and a completely bounded
and a completely bounded ![]() -bimodul-homomorphism, such that for all
-bimodul-homomorphism, such that for all ![]()