




Next: Smith's lemma
Up: Basic facts
Previous: Notations
Contents
Index
Examples
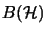 is an operator space by the identification
is an operator space by the identification
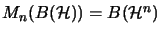 .
Generally, each
.
Generally, each
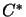 -algebra
-algebra 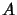 is an operator space if
is an operator space if 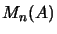 is
equipped with its unique
is
equipped with its unique 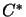 -norm.
Closed subspaces of
-norm.
Closed subspaces of
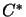 -algebras are called
concrete operator spaces.
Each concrete operator space is an operator space. Conversely, by the
theorem of Ruan , each operator space is completely isometrically
isomorphic to a concrete operator space.
-algebras are called
concrete operator spaces.
Each concrete operator space is an operator space. Conversely, by the
theorem of Ruan , each operator space is completely isometrically
isomorphic to a concrete operator space.
Commutative 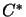 -algebras
are homogeneous operator spaces.
-algebras
are homogeneous operator spaces.
The transposition 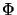 on
on 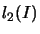 has norm
has norm
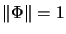 , but
, but
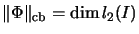 . If
. If 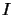 is infinite, then
is infinite, then 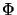 is bounded, but not completely bounded.
is bounded, but not completely bounded.
If
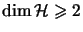 , then
, then 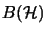 is
not homogeneous [Pau86, p. 6].
is
not homogeneous [Pau86, p. 6].
Prof. Gerd Wittstock
2001-01-07
![]() -algebras
are homogeneous operator spaces.
-algebras
are homogeneous operator spaces.
![]() on
on ![]() has norm
has norm
![]() , but
, but
![]() . If
. If ![]() is infinite, then
is infinite, then ![]() is bounded, but not completely bounded.
is bounded, but not completely bounded.
![]() , then
, then ![]() is
not homogeneous [Pau86, p. 6].
is
not homogeneous [Pau86, p. 6].