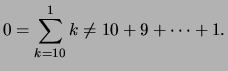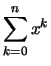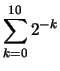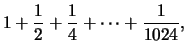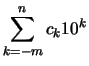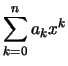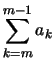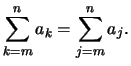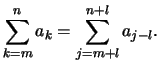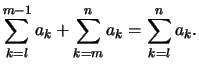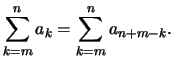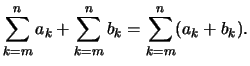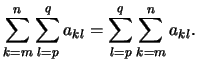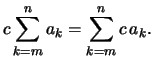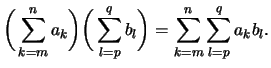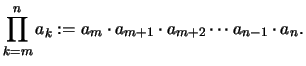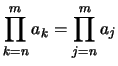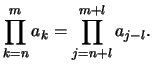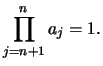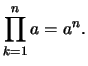Nächste Seite: Induktionsprinzip
Aufwärts: Vollständige Induktion
Vorherige Seite: Vollständige Induktion
Inhalt
Summen von endlich vielen reellen Zahlen nennt man im Unterschied zu den
noch zu behandelnden unendlichen Reihen auch endliche Summen oder
endliche Reihen.
Summen werden mit Hilfe des Summenzeichens abgekürzt:
Bezeichnung 1.2.1 (Summenzeichen)
- Es seien
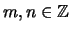 und
und 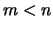 .
Wir schreiben die Summe der Zahlen
.
Wir schreiben die Summe der Zahlen
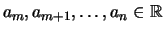 mit dem Summenzeichen:
mit dem Summenzeichen:
- Man nennt
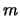 |
untere Summationsgrenze |
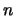 |
obere Summationsgrenze, |
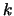 |
Laufindex oder Summationsindex, |
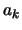 |
Summand. |
Die Anzahl der Summanden ist 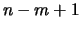 .
.
- Eine formale Erweiterung des Summenzeichens ist die leere Summe:
Eine Summe bei der der obere Summationsindex kleiner als der
untere Summationsindex ist, heißt leere Summe.
Die leere Summen wird als 0 definiert.
Bei der leeren Summe wird nichts addiert, die formalen Summanden müssen
nicht einmal definiert sein.
Ein Beispiel einer leeren Summe ist
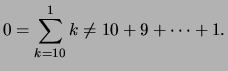
Feststellung 1.2.3 (Rechenregeln für endliche Summen)
- Auf die Bezeichnung des Index kommt es nicht an:
- Verschiebung des Laufindex:
Die Summationsgrenzen müssen entgegengesetzt verschoben werden.
- Das Assoziativgesetz gilt:
Wenn
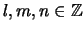 und
und 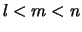 ist so gilt
Beachte, das Summenzeichen bindet stärker als das `
ist so gilt
Beachte, das Summenzeichen bindet stärker als das `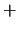 '-Zeichen.
'-Zeichen.
- Das Kommutativgesetz gilt:
Bei einer Umordnung (Permutation) der Summanden ändert sich der
Wert der Summe nicht.
- Beispiel: umgekehrte Reihenfolge der Summanden:
- Beispiel: Summen mit gleichen Summationsgrenzen kann man unter einem
Summenzeichen zusammenfassen:
- Beispiel: Bei Doppelsummen kann man die Summationsreihenfolge vertauschen:
Man ordne die Summanden in einem Rechteck an:
Man kann nun entweder zuerst die Zeilensummen bilden und diese aufaddieren
oder
mit den Spaltensummen beginnen.
Auf beiden Wegen erhält man die Summe aller Einträge.
- Das Distributivgesetz gilt:
- Beispiel: Für das Produkt zweier Summen gilt:
Man kann also auf die Klammern auf der linken Seite verzichten.
Produkte werden mit Hilfe des Produktzeichens abgekürzt:
Bezeichnung 1.2.4 (Produktzeichen)
- Es seien
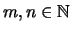 und
und 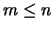 .
Wir schreiben das Produkt der Zahlen
.
Wir schreiben das Produkt der Zahlen
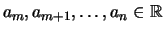 mit dem Produktzeichen:
mit dem Produktzeichen:
- Ein Produktzeichen, bei dem die obere Grenze kleiner als die untere Grenze
ist, heißt leeres Produkt.
Das leere Produkt wird als
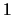 definiert.
definiert.
Bemerkungen und Beispiele 1.2.5 (Produktzeichen)
- Auf die Bezeichnung des Index kommt es nicht an; es ist:
- Der Laufindex läßt sich transformieren:
Die Grenzen müssen entsprechend transformiert werden.
- Das Produkt ist assoziativ und die Reihenfolge der Faktoren kann
beliebig permutiert werden.
- Beispiel eines leeren Produktes:
- Für
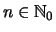 ,
,
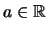 gilt
Für
gilt
Für 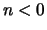 stimmt dies nicht!
stimmt dies nicht!
- Das Produkt der Zahlen
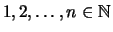 nennt man Fakultät von
nennt man Fakultät von 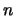 und bezeichnet es mit
und bezeichnet es mit 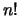 .
Man setzt
.
Man setzt 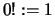 . Sprich:
. Sprich: 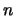 -Fakultät.
-Fakultät.
Es gilt für
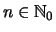 :
:




Nächste Seite: Induktionsprinzip
Aufwärts: Vollständige Induktion
Vorherige Seite: Vollständige Induktion
Inhalt
Analysis1-A.Lambert
2001-02-09
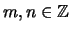 und
und 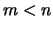 .
Wir schreiben die Summe der Zahlen
.
Wir schreiben die Summe der Zahlen
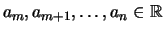 mit dem Summenzeichen:
mit dem Summenzeichen:
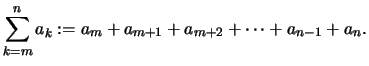
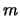
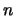
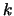
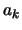
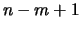 .
.