



Nächste Seite: Vollständigkeit der reellen Zahlen
Aufwärts: Konvergenz von Folgen
Vorherige Seite: Grenzwertregeln
Inhalt
Bemerkung.
1.) Statt 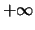 schreibt man auch
schreibt man auch 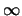 .
.
2.) Es sei 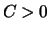 . Statt
. Statt 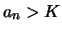 kann man auch
kann man auch
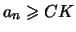 fordern.
fordern.
Bemerkung 2.1.23
Die Symbole
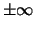
sind keine Zahlen. Man kann die Rechenregeln für
Grenzwerte bequem formulieren, wenn man
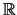
zu der Menge
erweitert und die folgenden Regeln vereinbart:
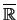
ist total geordnet.
Weitere Ausdrücke wie
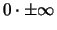
,
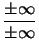
und
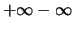
sind nicht definiert!
Bemerkung 2.1.26 (Wachstumsgeschwindigkeit)
Es ist für die Analysis sehr wichtig, die
Wachstumsgeschwindigkeit von Folgen
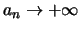
zu erfassen.
Eine Folge 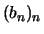 strebt schneller als
strebt schneller als 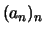 gegen
gegen
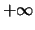 , falls
, falls
gilt.
Beispiel. In der folgenden Liste
strebt jede Folge schneller nach 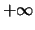 als die vorhergehende:
als die vorhergehende:
Zum Beweis siehe Beispiel ![[*]](crossref.png) ,
und Satz
,
und Satz ![[*]](crossref.png)




Nächste Seite: Vollständigkeit der reellen Zahlen
Aufwärts: Konvergenz von Folgen
Vorherige Seite: Grenzwertregeln
Inhalt
Analysis1-A.Lambert
2001-02-09
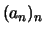 in
in
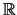 strebt gegen
strebt gegen 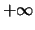 ,
falls es zu jedem
,
falls es zu jedem 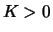 ein
ein
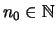 gibt, so daß für alle
gibt, so daß für alle
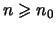 gilt:
Man schreibt
gilt:
Man schreibt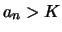 .
.
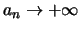 oder
oder
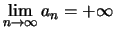 .
.
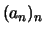 in
in
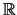 strebt gegen
strebt gegen 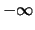 ,
falls es zu jedem
,
falls es zu jedem 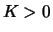 ein
ein
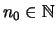 gibt, so daß für alle
gibt, so daß für alle
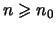 gilt:
Man schreibt
gilt:
Man schreibt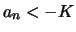 .
.
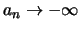 oder
oder
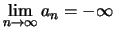 .
.
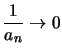 .
.![[*]](crossref.png)