



Nächste Seite: Monotone Folgen
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Vollständig geordneter Körper
Inhalt
Bei der Definition der Konvergenz muß man den Grenzwert bereits kennen,
um die Konvergenzbedingung nachzuprüfen.
Das Cauchysche Konvergenzkriterium ermöglicht, die Konvergenz einer
Folge zu testen, deren Grenzwert noch nicht bekannt ist.
Definition 2.2.7
Eine Folge
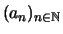
in
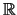
heißt
Cauchy-Folge, wenn gilt:
Augustin Louis Cauchy (1789-1857)
Bemerkung 2.2.8
Die Feststellungen
![[*]](crossref.png)
und
![[*]](crossref.png)
gelten sinngemäß auch für die Definition von Cauchy-Folgen.
Beispiel. Eine konvergente Folge 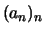 ist eine Cauchy-Folge:
ist eine Cauchy-Folge:
Es sei
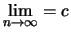 . Zu
. Zu
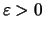 gibt es ein
gibt es ein
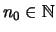 ,
so daß
,
so daß
Aus der Dreiecksungleichung folgt:
Satz 2.2.9 (Cauchysches Konvergenzkriterium)
Eine Folge
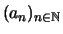
in
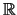
ist genau dann konvergent, wenn sie eine
Cauchy-Folge ist.
Beweis .
- Diese Beweisrichtung haben wir im obigen Beispiel gezeigt.

- Es sei
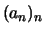 eine Cauchy-Folge.
Wir wählen zu den Vergleichswerten
eine Cauchy-Folge.
Wir wählen zu den Vergleichswerten
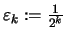 induktiv
passende
induktiv
passende
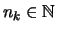 , so daß die Folge
, so daß die Folge 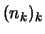 streng monoton
wachsend ist und
streng monoton
wachsend ist und
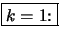
- Wähle zu
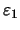 ein passendes
ein passendes 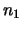 .
.
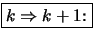
- Es seien zu
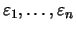 bereits
passende
bereits
passende 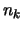 gefunden, so daß
gefunden, so daß
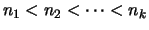 und (
und ( )
für
)
für
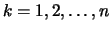 erfüllt ist.
erfüllt ist.
Dann gibt es nach Voraussetung zu
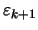 ein
ein 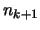 , so daß
, so daß
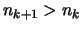 und (
und (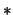 ) für
) für 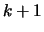 gilt.
gilt.
Man setze nun
![$\displaystyle I_k :=[a_{n_k}-2\varepsilon _k,a_{n_k}+2\varepsilon _k]$](img965.png) .
.
Nach Konstruktion ist
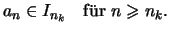
Es ist
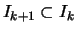 da (Zeichnung):
da (Zeichnung):
und folglich
![$\displaystyle [a_{n_{k+1}}-2\varepsilon _{k+1},a_{n_{k+1}}+2\varepsilon _{k+1}]
\subset[a_{n_k}-2\varepsilon _k,a_{n_k}+2\varepsilon _k]$](img975.png) .
.
Für die Längen der Intervalle gilt:
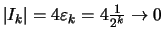 .
Nach dem Intervallschachtelungsprinzip
.
Nach dem Intervallschachtelungsprinzip
![[*]](crossref.png) gibt es ein
gibt es ein
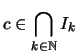 .
.
Wenn
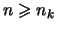 so sind
so sind
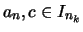 und folglich:
und folglich:
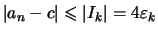 .
.
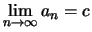 .
.
Bemerkung. Für die Konvergenz einer Folge reicht es nicht, daß die
Differenzen aufeinanderfolgender Glieder eine Nullfolge bilden:
- Für die harmonische Reihe
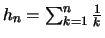 , (
, (
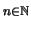 )
gilt
)
gilt
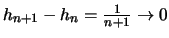 aber
aber
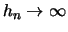 .
.
- Die Folge
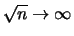 aber
aber
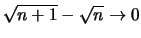 .
.
- Für die beschränkte Folge
bilden die Differenzen aufeinanderfolgender Glieder eine Nullfolge.
Die Folge ist aber nicht konvergent.
Wenn die die Differenzen aufeinanderfolgender Glieder einer Folge
kleiner sind als die Summanden einer konvergenten Reihe, so ist die Folge
eine Cauchyfolge.
Meistens vergleicht man mit der geometrischen Reihe:
Satz 2.2.10 (Vergleich mit geometrischer Reihe)
Wenn eine Folge
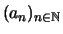 die folgende Bedingung erfüllt
die folgende Bedingung erfüllt
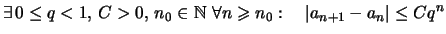 ,
,
dann ist sie konvergent.
Beweis . Die Folge ist eine Cauchyfolge.
Für 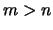 gilt
gilt




Nächste Seite: Monotone Folgen
Aufwärts: Vollständigkeit der reellen Zahlen
Vorherige Seite: Vollständig geordneter Körper
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() ist eine Cauchy-Folge:
ist eine Cauchy-Folge:
![]() . Zu
. Zu
![]() gibt es ein
gibt es ein
![]() ,
so daß
,
so daß
![]() ein
ein ![]() , so daß
, so daß
![]() und (
und (![]() ) für
) für ![]() gilt.
gilt.
![]() da (Zeichnung):
da (Zeichnung):
![[*]](crossref.png) gibt es ein
gibt es ein
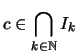 .
.
![]() die folgende Bedingung erfüllt
die folgende Bedingung erfüllt
![]() gilt
gilt
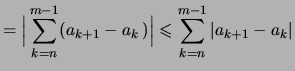
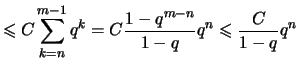 .
.