Supremum

Wir leiten ein weiteres Konstruktionsprinzip für reelle Zahlen her. Nicht jede beschränkte Teilmenge $M \subset \mathbb{R}$ hat Maximum und Minimum. Wir suchen für diesen Fall einen nützlichen Ersatz.

Ein Beispiel hierfür ist das offene Intervall $I = (0,\sqrt{2}) = \{ x\in\mathbb{R}\mid x>0,~ x^2 < 2\}$. Die Intervallenden $0$ und $\sqrt{2}$ sind ausgezeichnet:

-

Die reelle Zahl $\sqrt{2}$ ist die kleinste Zahl, die oberhalb von allen Punkten aus $I$ liegt, d. h. $\sqrt{2}$ ist die kleinste obere Schranke von $I$. Diese exisitiert aber nur in $\mathbb{R}$, nicht in $\mathbb{Q}$.

-

Die Zahl $0$ ist die größte untere Schranke von $I$.

Wir führen für den gesuchten Begriff kleinste obere Schranke eine Bezeichnung ein:

Definition 2.5.1 (Supremum)  

Es sei $M \subset \mathbb{R}$ nicht leer und nach oben beschränkt. Hat die Menge

$$S_M:=\{a\in\mathbb{R}\mid\:\forall x\in M :\; x\leq a\}$$

der oberen Schranken von $M$ ein Minimum $s$, so heißt $s$ kleinste obere Schranke oder Supremum von $M$ und wird mit

$$s = \sup{M}$$

bezeichnet.

Beispiel. Für das Intervall $I=(0,\sqrt{2})$ gilt $S_I=[\sqrt{2},\infty)$ und $\sup{I}=\min[\sqrt{2},\infty)=\sqrt{2}$.

Bemerkung 2.5.2  

1. Das Supremum einer Menge ist eindeutig bestimmt, da die Anordnung von $\mathbb{R}$ total ist (vgl. Feststellung und Bem. ).
2. Falls eine Menge ein Maximum besitzt, so stimmt dieses mit dem Supremum überein:
   $$\sup M = \max M$$.$$$$

Bezeichnung 2.5.3 (Infimum)  

Analog zur kleinsten oberen Schranke definiert man für eine nichtleere, nach unten beschränkte Menge $M \subset \mathbb{R}$ die größte untere Schranke.

Diese heißt Infimum von $M$ und wir mit

$$\inf M$$

bezeichnet.

Feststellung 2.5.4   Es sei $M \subset \mathbb{R}$ nicht leer und nach unten beschränkt. Bezeichnet $-M:=\{-x\mid x\in M\}$, so gilt

$$\inf{M}=-\sup(-M)$$.$$$$

Feststellung 2.5.5 (Charakterisierung des Supremums)  

Es sei $M \subset \mathbb{R}$ nicht leer und nach oben beschränkt. Es ist genau dann $s=\sup{M}$, wenn die folgenden beiden Bedingungen gelten:

1. $x\leqslant s$ für alle $x \in M$
2. Es gibt eine Folge $(x_n)$ in $M$, so daß $x_n\rightarrow s$.

Korollar 2.5.6  

Die Folge in (2.) kann monoton wachsend gewählt werden.

Beweis Satz .

Es sei $s=\sup M$. (1.) Dann ist $s$ eine obere Schranke.

(2.) Da $s$ kleinste obere Schranke ist, ist $s-\frac{1}{n}$ keine obere Schranke von $M$ und es gibt ein

$$x_n\in M$$   mit$$\quad s-\frac{1}{n} < x_n$$   .$$$$

Da $s-\frac{1}{n} < x_n \leqslant s$ ist, konvergiert die Folge $(x_n)_n$ gegen $s$.

Nach (1.) ist $s$ eine obere Schranke. Sei gemäß (2.)

$$(x_n)_n$$    in $$M$$   mit$$\quad \lim_{n\to\infty}x_n = s$$   .$$$$

Dann gibt es zu jedem $t<s$ ein $n_0\in\mathbb{N}$, so daß für $n\geqslant n_0$:

$$\vert s-x_n\vert< s-t,$$   folglich$$\quad t < x_n$$   .$$$$

Also ist $t$ keine obere Schranke von $M$, d. h. $s$ ist die kleinste obere Schranke von $M$.

Beweis Korollar .

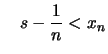Man setze (vgl. Feststellung )

$$y_n :=\max\{x_1,\dots,x_n\}$$   .$$$$

Die Folge $(y_n)_n$ liegt in $M$, ist monoton wachsend und konvergiert ebenfalls gegen $s$.

Aus der Grenzwertregel für Folgen ergibt sich die Bemerkung:

Bemerkung 2.5.7 (Grenzwert oberer Schranken)  

Es sei $M \subset \mathbb{R}$ nicht leer. Wenn $(s_n)_n$ eine konvergente Folge von oberen Schranken von $M$ ist, so ist auch der Grenzwert eine obere Schranke von $M$.

Aus den Axiomen

(A)

Archimedisches Axiom

(I)

Intervallschachtelungsprinzip

ergibt sich nun die Supremums-Eigenschaft (S):

Satz 2.5.8 (Supremumseigenschaft von $\mathbb{R}$)  

Jede nichtleere, nach oben beschränkte Teilmenge von $\mathbb{R}$ hat eine kleinste obere Schranke $\sup M \in \mathbb{R}$.

Anmerkung. 1. Umgekehrt folgen aus der Supremums-Eigenschaft das Archimedische Axiom und das Intervallschachtelungsprinzip.

2. Zum Beweis konstruieren wir induktiv mit der Methode der Intervall-Halbierung eine Intervallschachtelung.

Beweis . Wir konstruieren induktiv zwei monotone Folgen $(x_n)_n$ in $M$ und $(s_n)_n$ in $S_M$, so daß für $n\in\mathbb{N}_0$ gilt:

$$s_{n+1} -x_{n+1} \leqslant \frac{1}{2}(s_n-x_n)$$        $(\star)$$$$$

Startwerte:

Wähle $x_0\in M$ und $s_0\in S_M$.

Iteration:

Es seien bereits   $x_1\leqslant x_2 \leqslant \dots \leqslant x_n$  in $M$ und $s_1\geqslant s_2 \geqslant \dots \geqslant s_n$ in $S_M$ gewählt, so daß $(\star)$ gilt.

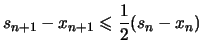
Dann setze man $y_{n} :=\frac{1}{2}(x_n+s_n)$. Es gibt zwei Fälle

$y_n\in S_M$:

Setze $x_{n+1}:=x_n$, $s_{n+1}:=y_n$.

Dann ist $s_{n+1}-x_{n+1} = \frac{1}{2}(s_n-x_n)$.

$y_n \not\in S_M$:

Wähle $x_{n+1}\in M$ mit $y_n<x_{n+1}$ und $s_{n+1}:=y_n$.

Dann ist $s_{n+1}-x_{n+1} \leqslant s_n-y_n = \frac{1}{2}(s_n-x_n)$.

Die beiden Folgen $(x_n)_n$ und $(s_n)_n$ bilden wegen $(\star)$ eine Intervallschachtelung und konvergieren gegen den gleichen Wert $s \in S_M$. Nach Feststellung ist $s=\sup M$.