Es seien ![]() ,
,
![]() nichtausgeartete Intervalle und
nichtausgeartete Intervalle und
![]() eine streng monoton wachsende Funktion
mit Umkehrfunktion
eine streng monoton wachsende Funktion
mit Umkehrfunktion
![]() .
.
Dann sind ![]() und
und ![]() stetig.
stetig.
Es seien ![]() ,
,
![]() nichtausgeartete Intervalle und
nichtausgeartete Intervalle und
![]() eine streng monoton wachsende Funktion
mit Umkehrfunktion
eine streng monoton wachsende Funktion
mit Umkehrfunktion
![]() .
.
Dann sind ![]() und
und ![]() stetig.
stetig.
Anmerkung
Beispiele
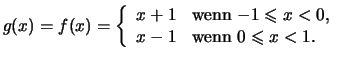
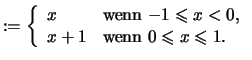 |
||
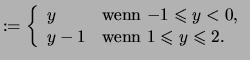 |
Beweis (Stetigkeit der Umkehrfunktion).
Wir zeigen die Stetigkeit der Umkehrfunktion ![]() (vgl. Satz
(vgl. Satz ![[*]](crossref.png) ).
).
Es seien ![]() ,
,
![]() und
und
![]() .
Es sei
.
Es sei
![]() der linke Endpunkt von
der linke Endpunkt von ![]() und
und
![]() der rechte Endpunkt.
Man setze
der rechte Endpunkt.
Man setze
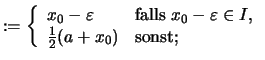 |
||
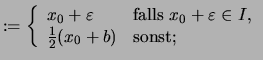 |
||
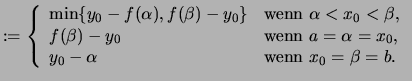 |
und somit
![]() .
.
Aus Satz ![[*]](crossref.png) und Korollar
und Korollar ![[*]](crossref.png) folgt nun:
folgt nun:
Sei
![]() ein Intervall und
ein Intervall und
![]() eine stetige und streng monotone Funktion.
Dann ist die Umkehrfunktion
eine stetige und streng monotone Funktion.
Dann ist die Umkehrfunktion
![]() stetig, wobei
stetig, wobei ![]() .
.
Wir betrachten zunächst den Fall ![]() .
.
Wenn ![]() , so ist
, so ist ![]() streng monoton wachsend.
streng monoton wachsend.
Beweis . Annahme: ![]() ist nicht strikt monoton wachsend:
ist nicht strikt monoton wachsend:
Dann gibt es Punkte ![]() ,
,
![]() mit
mit ![]() und
und
![]() .
Da
.
Da ![]() injektiv, ist
injektiv, ist
![]() .
Wir unterscheiden zwei Fälle:
.
Wir unterscheiden zwei Fälle:
![[*]](crossref.png)
Da
![]() , widerspricht das der Injektivität von
, widerspricht das der Injektivität von ![]() .
.
![[*]](crossref.png)
Da
![]() , widerspricht das der Injektivität von
, widerspricht das der Injektivität von ![]() .
.
Beweis . Wähle ![]() ,
, ![]() mit
mit ![]() .
.
Wir zeigen, wenn
![]() , dann ist
, dann ist ![]() streng monoton wachsend:
streng monoton wachsend:
Seien,
mit
. Man setze
Nach dem vorangehenden Lemma ist die Einschänkungentweder streng monoton wachsend oder fallend, je nachdem ob
oder
ist.
Daund
ist, muß die Einschränkung
streng monoton wachsend sein.
DaWennist, folgt
.
Beispiel (Logarithmus).
Für
![]() ,
, ![]() ist die Exponentialfunktion zur Basis
ist die Exponentialfunktion zur Basis ![]() :
:
Für
![]() ,
, ![]() ist die Exponentialfunktion zur Basis
ist die Exponentialfunktion zur Basis ![]() :
:
Es sei
![]() ,
, ![]() .
Die Umkehrfunktion der Exponentialfunktion zur Basis
.
Die Umkehrfunktion der Exponentialfunktion zur Basis ![]() heißt Logarithmus zur Basis
heißt Logarithmus zur Basis ![]() :
:
Die Umkehrfunktion der Exponentialfunktion
![]() heißt natürlicher Logarithmus oder kurz der Logarithmus
und wird mit
heißt natürlicher Logarithmus oder kurz der Logarithmus
und wird mit
Mathematiker schreiben meistens ![]() , Physiker
und Ingenieure
, Physiker
und Ingenieure ![]() .
.
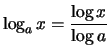 für
für
Anmerkung. Wir werden noch weitere wichtige Eigenschaften der Exponentialfunktion und des Logarithmus in den folgenden Kapiteln kennenlernen.