Funktionenfolgen

Bezeichnung 2.8.1 (Menge von Funktionen)  

Für eine Menge $M$ bezeichne $\mathcal{F}(M)=\mathcal{F}(M,\mathbb{R})$ die Menge aller Funktionen von $M$ nach $\mathbb{R}$.

Definition 2.8.2 (Folge von Funktionen)  

Eine Abbildung

$$f:\mathbb{N}\to\mathcal{F}(M)$$

heißt Folge von Funktionen oder Funktionenfolge.

Die Abbildungswerte $f_n:=f(n)$ heißen Folgenglieder, und man schreibt

$$(f_n)_n = (f_n)_{n\in\mathbb{N}} :=f$$   .$$$$

Bemerkung. Wenn $(f_n)_n$ eine Folge von Funktionen in $\mathcal{F}(M)$ ist, so bilden für jedes $x \in M$ die Funktionswerte eine Folge $(f_n(x))_n$ reeller Zahlen.

Definition 2.8.3 (Punktweise Konvergenze)  

Eine Funktionenfolge $(f_n)$ in $\mathcal{F}(M)$ konvergiert punktweise auf $M$ gegen $f\in\mathcal{F}(M)$, falls für alle $x \in M$

$$\lim\limits_{n\to\infty}f_n(x)=f(x)$$.$$$$

Das heißt:

$$\forall x\in M\ \forall\varepsilon >0\ \exists n_0\in\mathbb{N}\ \forall n\geqslant n_0 \quad:\quad \vert f_n(x)-f(x)\vert<\varepsilon$$   .$$$$

Bemerkung. Wenn eine Funktionenfolge $(f_n)_n$ für alle $x \in M$ einen Grenzwert in $\mathbb{R}$ hat, so definiert dies eine Funktion $f:M\rightarrow \mathbb{R}$ durch

$$f(x) :=\lim_{n\to\infty} f_n(x)$$.$$$$

Die Folge $(f_n)_n$ konvergiert punktweise gegen $f$.

Beispiele 2.8.4   Man zeichne die Graphen der folgenden Funktionen:

1. Für die Folge $(f_n)_n$ von Funktionen auf dem Intervall $[0,1]$ mit $f_n(x) :=x^n$, $x \in [0,1]$ gilt
   $$\lim_{n\to\infty} f_n(x) = \left\{ \begin{array}{ll} 0& \text{f\uml ur \( x\in[0,1) \),}\\ 1& \text{f\uml ur \( x=1 \).} \end{array}\right.$$

2. Für die Folge $(g_n)_n$ mit $$g_n(x) :=\frac{nx}{1+n\vert x\vert}$$, $(x\in\mathbb{R})$, gilt
   $$\lim_{n\to\infty} g_n(x) = \left\{ \begin{array}{ll} 1& \text{f\u... ...ext{f\uml ur \( x=0 \),}\\ -1& \text{f\uml ur \( x<0 \).} \end{array}\right.$$

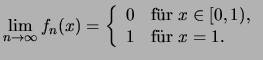
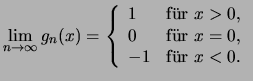
3. $h_n(x) = \left\{\begin{array}{ll} nx& \text{f\uml ur \( x\in[0,\frac{1}{n}] \)... ...= 0 \).}\\ 0& \text{f\uml ur \( x\in(\frac{2}{n},1] \).} \end{array} \right.$

Bemerkung. Es stellt sich die Frage, welche Eigenschaften der Glieder einer konvergenten Funktionenfolge sich auf die Grenzfunktion übertragen.

Die Beispiele (1.) und (2.) zeigen, daß bei punktweiser Konvergenz die Stetigkeit sich nicht auf die Grenzfunktion vererbt.

Wir müssen den Konvergenzbegriff für Funktionenfolgen verschärfen, um aus Eigenschaften der Folgenglieder auf entsprechende Eigenschaften der Grenzfunktion schließen zu können.

Im Beispiel (3.) konvergiert die Folge $(h_n)_n$ zwar punktweise gegen die konstante Funktion $0$, aber die $h_n$ sind offensichtlich keine gute Approximation der Grenzfunktion.

Noch krasser ist das Beispiel $d_n(x) :=n\,h_n(x)$.

Definition 2.8.5 (Gleichmäßige Konvergenz)  

Eine Funktionenfolge $(f_n)$ in $\mathcal{F}(M)$ konvergiert gleichmäßig auf $M$ gegen eine Grenzfunktion $f\in\mathcal{F}(M)$, falls es zu jedem $\varepsilon >0$ ein $n_0\in\mathbb{N}$ gibt, so daß für alle $n\in \mathbb{N}$ und für alle $x \in M$ aus $n\geqslant n_0$ stets

$$\vert f_n(x)-f(x)\vert < \varepsilon$$

folgt. In Zeichen:

$$\forall\varepsilon >0\ \exists n_0\in\mathbb{N}\ \forall n\geqslant n_0\ \forall x\in M \ :\ \vert f_n(x)-f(x)\vert<\varepsilon$$   .$$$$

Bemerkung Man vergleiche dies mit der punktweisen Konvergenz:

$$\forall x\in M\ \forall\varepsilon >0\ \exists n_0\in\mathbb{N}\ \forall n\geqslant n_0 \ :\ \vert f_n(x)-f(x)\vert<\varepsilon$$   .$$$$

Satz 2.8.6 (Stetigkeit der Grenzfunktion)  

Für ein Intervall $I\subseteq \mathbb{R}$ konvergiere die Funktionenfolge $(f_n)$ in $\mathcal{F}(I)$ gleichmäßig auf $I$ gegen $f\in\mathcal{F}(I)$. Sind alle $f_n$ in einem Punkt $a\in I$ stetig, so gilt dies auch für die Grenzfunktion $f$.

Bemerkung. Der Satz gilt entsprechend auch für die rechts- bzw. linksseitige Stetigkeit in $x_0$.

Beweis (Stetigkeit der Grenzfunktion).

Es sei $\varepsilon >0$. Da die Folge $(f_n)_n$ gleichmäßig gegen die Grenzfunktion $f$ konvergiert, gibt es ein $n_0\in\mathbb{N}$, so daß für alle $n\geqslant n_0$ und für alle $x \in M$

$$\vert f_n(x)-f(x)\vert < \varepsilon$$

ist. Da $f_{n_0}$ in $x_0$ stetig ist, gibt es ein $\delta>0$, so daß für jedes $x \in M$ aus $\vert x-x_0\vert < \delta$ stets

$$\vert f_{n_0}(x)-f_{n_0}(x_0)\vert < \varepsilon$$

folgt. Dann gilt für $x \in M$ mit $\vert x-x_0\vert < \delta$:

$$\vert f (x)-f(x_0)\vert$$

$$= \vert f(x)-f_{n_0}(x)+(f_{n_0}(x)-f_{n_0}(x_0)+f_{n_0}(x_0)-f(x_0)\vert$$

$$\leqslant\vert f(x)-f_{n_0}(x)\vert+\vert f_{n_0}(x)-f_{n_0}(x_0)\vert +\vert f_{n_0}(x_0)-f(x_0)\vert$$

$$< \varepsilon +\varepsilon +\varepsilon = 3\,\varepsilon$$

Bezeichnung 2.8.7   Die Menge der beschränkten Funktionen auf einer Menge $M$ wird mit

$$\mathcal{B}(M):=\{f\in\mathcal{F}(M)\mid$$   $f$ beschränkt$$\}$$

bezeichnet

Definition 2.8.8 (Norm einer Funktion)  

Es sei $M$ eine Menge. Die Norm einer beschränkten Funktion $f:M\to\mathbb{R}$ wird definiert durch

$$\Vert f\Vert:=\sup_{x\in M}\vert f(x)\vert:=\sup\{\vert f(x)\vert\;\vert\;x\in M\}$$.

Feststellung 2.8.9   Die Norm

$$\Vert.\Vert : \mathcal{B}(M)\rightarrow \mathbb{R}$$

hat die folgenden Eigenschaften:

Für $f$, $g\in \mathcal{B}(M)$ und $\alpha\in\mathbb{R}$ gilt:

1. $\ \Vert f\Vert\geqslant 0$, und $\Vert f\Vert=0$ genau dann, wenn $f=0$,
2. $\ \Vert\alpha f\Vert=\vert\alpha\vert\Vert f\Vert$,
3. $\ \Vert f+g\Vert\leqslant\Vert f\Vert+\Vert g\Vert$,
4. $\ \Vert f\cdot g\Vert\leqslant\Vert f\Vert\cdot\Vert g\Vert$.

Feststellung 2.8.10   Es sei $f\in\mathcal{F}(M)$. Eine Funktionenfolge $(f_n)$ in $\mathcal{F}(M)$ konvergiert genau dann gleichmäßig gegen $f$, wenn gilt:

$$\lim\limits_{n\to\infty}\Vert f_n-f\Vert=0$$   .

Beweis .

Die Folge $(f_n)_n$ konvergiere gleichmäßig gegen $f$. Es gibt also zu $\varepsilon >0$ ein $n_0\in\mathbb{N}$, so daß

$$\vert f_n(x)-f(x)\vert \leqslant \varepsilon$$   für alle $n\geqslant n_0$.$$$$

Nach Definition der Norm folgt für alle $n\geqslant n_0$:

$$\Vert f_n-f\Vert = \sup_{x\in M}\vert f_n(x)-f(x)\vert \leqslant \varepsilon$$   .$$$$

Es gelte $\lim\limits_{n\to\infty}\Vert f_n-f\Vert =0$. Dann gibt es zu $\varepsilon >0$ ein $n_0\in\mathbb{N}$, so daß aus $n\geqslant n_0$ stets $\Vert f_n-f\Vert< \varepsilon$ folgt. Also gilt für $n\geqslant n_0$ und alle $x \in M$:

$$\vert f_n(x)-f(x)\vert \leqslant \Vert f_n-f\Vert< \varepsilon$$   .$$$$

Satz 2.8.11   Cauchykriterium:

Eine Funktionenfolge $(f_n)$ in $\mathcal{F}(M)$ konvergiert genau dann gleichmäßig auf $M$, wenn gilt:

$$\forall\varepsilon >0\ \exists n_0\in\mathbb{N}\ \forall n,m\geqslant n_0\ :\ \Vert f_n-f_m\Vert<\varepsilon$$   .$$$$

Beweis .

Die Folge $(f_n)_n$ konvergiere gleichmäßig gegen $f$. Es gibt also zu $\varepsilon >0$ ein $n_0\in\mathbb{N}$, so daß

$$\vert f_n(x)-f(x)\vert \leqslant \varepsilon$$   für alle $n\geqslant n_0$.$$$$

Nach Definition der Norm folgt für alle $n$, $m \geqslant n_0$:

$$\Vert f_n-f\Vert = \sup_{x\in M}\vert f_n(x)-f(x)\vert \leqslant \varepsilon$$

$$\Vert f_n - f_m\Vert \leqslant\Vert f_n-f\Vert +\Vert f-f_m\Vert \leqslant 2\,\varepsilon$$

Wenn $\Vert f_n-f_m\Vert < \varepsilon$ für alle $m$, $n\geqslant n_0$ ist, dann folgt für alle $x \in M$:

$$\vert f_n(x)-f_m(x)\vert \leqslant \Vert f_n-f_m\Vert< \varepsilon$$   .$$$$

Daher ist $(f_n(x))_n$ eine Cauchyfolge in $\mathbb{R}$ und es gibt eine Grenzfunktion $f\in\mathcal{F}(M)$. Nun folgt für $n\geqslant n_0$

$$\vert f_n(x)-f(x)\vert = \lim_{m\to\infty}\vert f_n(x)-f_m(x)\vert \leqslant \varepsilon$$   .$$$$