Mathematik für Informatiker I
Prof . Dr. F.-O. Schreyer
Eingangstest
Abgabetermin 29.10.2002 vor der Vorlesung
Wir gehen von einer Bearbeitungszeit von 2 Stunden aus. Dieser Test soll einen
Überblick über das vorhandene Wissen der Vorlesungsteilnehmer geben
und geht nicht in die Bewertung ein, bitte nicht abschreiben!
Verwenden Sie bitte für jede Aufgabe ein eigenes Blatt (am besten das Angabenblatt).
- Zeigen Sie: Durch 3 Punkte in der Ebene, die nicht auf einer Geraden
liegen, geht
genau 1 Kreis.
- Berechnen Sie den Abstand der windschiefen Geraden im
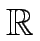 3
3
l1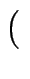 t t |
= 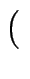 1, t, t 1, t, t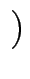 , t , t 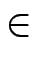  |
|
l2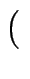 t t |
= 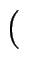 t, - t, 1 t, - t, 1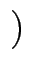 , t , t 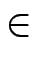  |
|
- 3.
- Diskutieren Sie die Funktion
y =
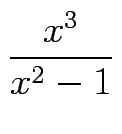
(Nullstellen, Maxima, Minima, Wendepunkte, Asymptoten) und fertigen Sie eine
qualitativ korrekte Skizze an.
- 4.
- Wie groß ist die durch die Graphen der Funktionen
eingeschlossene Fläche?
- 5.
- Lösen Sie das lineare Gleichungssystem:
| x1 + x2 + x3 |
= 1 |
|
| x1 +2x2 +3x3 |
= 4 |
|
| x1 +4x2 +9x3 |
= 16 |
|
- 6.
- Sei q ein Quadrat. Wieviele Elemente enthält die Gruppe der
Symmetrien von q?
- 7.
- Wie groß ist die Chance 6 Richtige beim Lotto zu tippen?
- 8.
- Seien x1 und x2 zwei Augenzahlen beim Würfeln. Wie
groß ist der Erwartungswert der Funktion
 x1
x1 +
x2 - 7
janko
2002-10-21
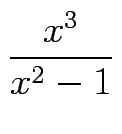
![\includegraphics[
height=0.435in,
width=0.4454in
]{quadrat.eps}](images/img11.gif)