- Man nehme Thymian und dazu von Majoran und Salbei mindestens ein
Gewürz.
- Man nehme sowohl Salbei als auch Majoran.
- Man nehme sowohl Oregano als auch Chilipulver.
- Man nehme weder Salbei noch Thymian und von Oregano und Chilipulver
allenfalls eines.
- Man nehme weder Oregano noch Majoran.
- Man nehme weder Chilipulver noch Salbei.
Dazu der Kommentar des Kochs:
''Wenn man jede einzelne dieser Vorschriften nicht befolgt, dann hat man das richtige Rezept.''
Wie würzt er seine Bratensoße?
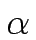 .
.-
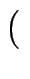 A
A 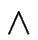
 C
C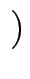
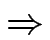
 B
B
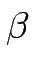 .
.-
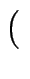
 A
A 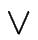 B
B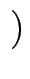
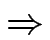
 C
C
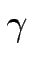 .
.-

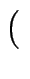
 A
A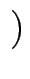
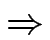
 C
C 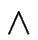
 B
B
mit
| A : Der Herbst ist sonnig |
| B : Der Wein ist teuer |
| C : Der Ertrag ist gering |
Übersetzen Sie
![]() ,
,![]() und
und ![]() jeweils eine umgangssprachliche
Formulierung. Welche Aussagen machen Sinn?
jeweils eine umgangssprachliche
Formulierung. Welche Aussagen machen Sinn?
Negieren Sie
![]() ,
,![]() und
und ![]() .
.
Formulieren Sie auch die Negation umgangssprachlich.
Hinweis: Betrachten Sie eine geeignete Menge von Paaren und verwenden Sie das Schubfachprinzip.
- Zeigen Sie mit vollständiger Induktion:
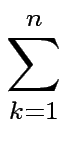 k2 =
k2 = 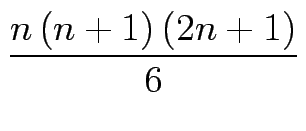
- Stellen Sie eine Formel für
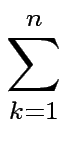 k3
k3
auf, und beweisen Sie diese.
![\includegraphics[
height=2.0928in,
width=3.0952in
]{gitter.eps}](images/img16.gif)
Beweisen Sie die Formel mit vollständiger Induktion.