Sei
p![]() x
x![]() : = adxd + ... + a1x + a0
: = adxd + ... + a1x + a0 ![]()
![]() [x]
[x]
ein Polynom vom Grad d, welches für große
n ![]()
![]() ganzzahlige Werte annimmt, d.h.
ganzzahlige Werte annimmt, d.h.
![]() n0, sodaß gilt
p
n0, sodaß gilt
p![]() n
n![]()
![]()
![]()
![]() n
n ![]() n0.
n0.
Zeigen Sie ![]()
![]() ,...,
,...,![]()
![]()
![]() , sodaß
, sodaß
![$\displaystyle \binom{%%
\begin{tabular}[c]{lll}%%
$x$\ & $+$\ & $k$%%
\end{tabular}}{k}%%
$](images/img17.gif)
![$\displaystyle \binom{%%
\begin{tabular}[c]{lll}%%
$x$\ & $+$\ & $k$%%
\end{tabular}}{k}$](images/img18.gif) : =
: = 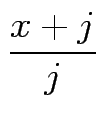
Hinweis: Verwenden Sie Induktion nach d und das Differenzenpolynom
![]() p
p ![]()
![]() [x] definiert für
p
[x] definiert für
p ![]()
![]() [x] durch
[x] durch
- Wir definieren die folgende Äquivalenzrelation auf
M : =
 ×
× durch
durch
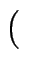 a, b
a, b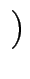
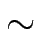
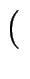 c, d
c, d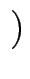 genau
dann, wenn a + d = b + c.
genau
dann, wenn a + d = b + c.
- Zeigen Sie, daß dies eine Äquivalenzrelation auf M ist.
- Beschreiben Sie die Äquivalenzklassen
[
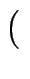 1, 1
1, 1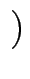 ] und
[
] und
[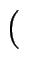 3, 1
3, 1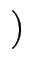 ].
].
- Definieren Sie die Addition von Äquivalenzklassen durch
[Zeigen Sie, daß diese Addition wohldefiniert ist, d.h. unabhängig von den gewählten Repräsentanten der Äquivalenzklassen ist.
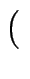 a, b
a, b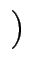 ] + [
] + [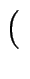 c, d
c, d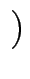 ] : = [
] : = [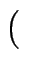 a + c, b + d
a + c, b + d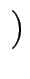 ]
]
- Zeigen Sie
[
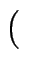 a, b
a, b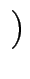 ] + [
] + [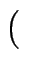 2, 2
2, 2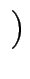 ] = [
] = [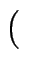 a, b
a, b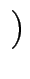 ] und
[
] und
[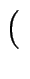 2, 5
2, 5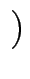 ] + [
] + [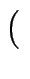 7, 5
7, 5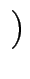 ] = [
] = [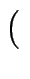 1, 2
1, 2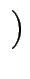 ]
]
- Kennen Sie die Menge der Äquivalenzklassen M/
 unter anderem Namen?
unter anderem Namen?
- Zeigen Sie, daß dies eine Äquivalenzrelation auf M ist.
- Betrachte Sie die Menge
M : =
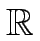 2\
2\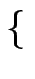
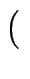 0, 0
0, 0
 , d.h. die Menge aller Punkte der reellen Ebene ohne
den 0-Punkt.
, d.h. die Menge aller Punkte der reellen Ebene ohne
den 0-Punkt.
Wir definieren eine Äquivalenzrelation auf M×M durch
 x, y
x, y
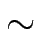
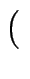 x
x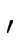 , y
, y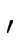
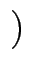 genau dann, wenn es
eine Gerade durch den Nullpunkt
genau dann, wenn es
eine Gerade durch den Nullpunkt
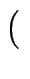 0, 0
0, 0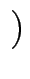
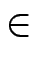
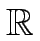 2 gibt,
auf der sowohl der Punkt
2 gibt,
auf der sowohl der Punkt
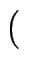 x, y
x, y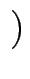 als auch der Punkt
als auch der Punkt
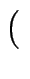 x
x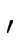 , y
, y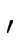
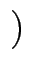 liegen.
liegen.
- Zeigen Sie, daß dies tatsächlich eine Äquivalenzrelation ist.
- Finden Sie eine geometrische Darstellung der Menge der
Äquivalenzklassen M/
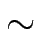 indem Sie in jeder Äquivalenzklasse einen
geeigneten Repräsentanten wählen.
indem Sie in jeder Äquivalenzklasse einen
geeigneten Repräsentanten wählen.
- Zeigen Sie, daß dies tatsächlich eine Äquivalenzrelation ist.
- Es gibt keine surjektive Abbildung
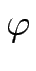 : M
: M  2M.
2M.
- Es gibt keine injektive Abbildung
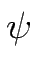 : 2M
: 2M  M.
M.
| x | ||
| x | ||
| x |
- Programmieren Sie in Maple eine Funktion ggT, die für zwei ganze
Zahlen a, b eine Darstellung
ggTmit u, v
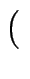 a, b
a, b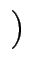 = u . a + v . b
= u . a + v . b
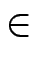
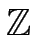 berechnet und die Liste
[ggT
berechnet und die Liste
[ggT a, b
a, b , u, v] zurückgibt.
, u, v] zurückgibt.
Bem.: Verwenden Sie proc zur Definition einer Prozedur und iquo zur Division mit Rest. Vergleichen Sie an Beispielen ihre Funktion mit der eingebauten Maple-Prozedur igcdex.
- Scheiben Sie eine Maple-Funktion, die den
ggT
 L
L für eine Liste von ganzen Zahlen
L = [a1,..., ak] bestimmt.
für eine Liste von ganzen Zahlen
L = [a1,..., ak] bestimmt.
(Abgabe bitte als Ausdruck mit einer Beispielrechnung).