Mathematik für Informatiker I
Prof . Dr. F.-O. Schreyer
Übungsblatt 3
Abgabetermin Montag 18.11.2002 vor der Vorlesung
- Bestimmen Sie sämtliche Untergruppen der S4 mit Hilfe des
Tetraeders (Typ der
Untergruppe und die Anzahl der Untergruppen der
gleichen Art)
- Zeigen Sie:
Ist G eine Gruppe der Ordnung
pl . m, wobei p eine Primzahl ist,
die nicht m teilt, und l 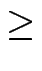 1, dann hat G eine Untergruppe der Ordnung
pl.
1, dann hat G eine Untergruppe der Ordnung
pl.
- Zeigen Sie:
Sind
a, b 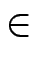
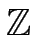 mit a, b
mit a, b 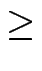 1 und
ggT
1 und
ggT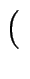 a, b
a, b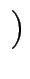 = 1. Dann
gilt
= 1. Dann
gilt
- Sei
G : =
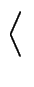 s1
s1,...,
sn-1 |
si2 =
e,
sisj =
sjsi falls
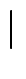 i
i -
j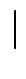

2,
sisi+1si =
si+1sisi+1 i
i,
j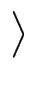
Zeigen Sie
G 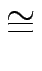 Sn
Sn
- Bestimmen die Symmetriegruppen W, O, D und I von Würfel,
Oktaeder, Dodekaeder und Ikosaeder:
Hinweise:
- Ermitteln Sie zunächst die Gruppenordnung.
- Beachten Sie:
und so weiter.
janko
2002-11-08
![\includegraphics[
height=1.8395in,
width=1.9943in
]{tetrah.eps}](images/img1.gif)
![]() 1, dann hat G eine Untergruppe der Ordnung
pl.
1, dann hat G eine Untergruppe der Ordnung
pl.
![]()
![]() mit a, b
mit a, b ![]() 1 und
ggT
1 und
ggT![]() a, b
a, b![]() = 1. Dann
gilt
= 1. Dann
gilt
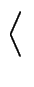 s1,..., sn-1 | si2 = e, sisj = sjsi falls
s1,..., sn-1 | si2 = e, sisj = sjsi falls 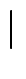 i - j
i - j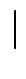
 2, sisi+1si = si+1sisi+1
2, sisi+1si = si+1sisi+1 i, j
i, j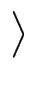
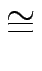 Sn
Sn
![$\displaystyle \begin{array}[c]{cc}%%
{\includegraphics[
height=2.4267in,
width=...
...n 0.000000in,
height=1.8836in,
width=1.7106in
]%%
{octah.eps}%%
}%%
\end{array}$](images/img17.gif)
![\includegraphics[
height=1.9424in,
width=2.1672in
]{dodah.eps}](images/img18.gif)
![\includegraphics[
trim=0.009564in -0.215925in 0.014745in 0.000000in,
height=1.8204in,
width=1.4875in
]{icosah.eps}](images/img19.gif)
![\includegraphics[
height=2.4258in,
width=2.1214in
]{polydual.eps}](images/img20.gif)