- Zeigen Sie: Es gibt keinen Körper mit genau 6 Elementen.
- Gibt es einen Körper mit genau 4 Elementen?
![\includegraphics[
height=1.0654in,
width=1.0654in
]{spiel2.eps}](images/img1.gif)
![\includegraphics[
height=1.0654in,
width=1.0654in
]{spiel1.eps}](images/img2.gif)
überführen?
- Welche Ordnungen treten bei den Elementen von S7 auf?
- Sei
G
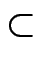 Sn eine Untergruppe mit
Sn eine Untergruppe mit
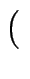 1, 2
1, 2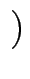
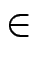 G
und
G
und
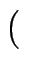 1, 2,..., n
1, 2,..., n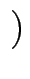
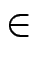 G. Zeigen Sie
G = Sn
G. Zeigen Sie
G = Sn
-
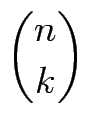
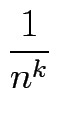
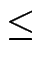
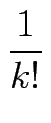 für allek
für allek 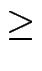 0
0
-
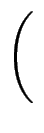 1 +
1 + 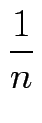
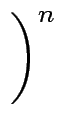
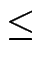
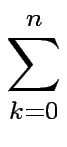
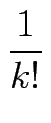 < 3
< 3
-
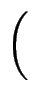
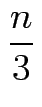
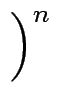
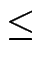
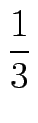 n!
n!