![]()
 |
Universität
des Saarlandes Mathematik und Informatik Prof. Dr. Frank-Olaf Schreyer |
Tel.:
+49 (0)681/302-2785 schreyer@math.uni-sb.de Zi. 425, Geb. 27 D-66123 Saarbrücken |
Visualisierung von Raumkurven
Projekt im Softwarepraktikum WS 03/04
Thema
Wenn wir eine reelle Kurve im 3-dimensionalen Raum durch Gleichungen oder eine Parametrisierung gegeben haben, stellt sich die Frage, wie diese Kurve nun im Raum dargestellt aussieht. Denn die Gleichungen alleine geben wenig Aufschluss darüber, an welchen Stellen sich interessante Punkte oder Kurvenabschnitte befinden. Hat man eine Kurve visualisiert vor Augen, gelangt man zu ganz anderen Einsichten und Ideen, was man mit der Kurve nicht alles anfangen könnte. Dafür benötigt man Tools, die eine gegebene Raumkurve dreidimensional visualisieren. Neben der wissenschaftlichen Anwendung werden solcheTools auch in der Schule zur Entwicklung des Raumverständnisses verwendet.
In diesem Sinne wollen wir im Praktikum ein Programm entwickeln, das eine durch Formeln beschriebenen Raumkurve im Rechner darstellt, die Zeichnung auf den (leider nur 2-dimensionalen) Bildschirm projiziert und auch die Möglichkeit der Betrachtung mit 3-D-Brille bietet.
Die Kurve ist entweder durch eine Parametrisierung gegeben, d.h. man hat für jeden der drei Raumkoordinaten eine Formel, um aus einem Parameter die Koordinaten zu berechnen (ein simples Beispiel: (x(t),y(t),z(t))=(5 t, 0, t) ), oder aber implizit d.h. durch Gleichungen in den drei Raumkoordinaten, die genau auf den Punkten der Kurve null sein sollen (z.B. X - 5Z = 0 und Y = 0, was übrigens genau die Kurve von eben ist). Da man nicht jede durch Gleichungen gegebene Kurve durch eine Parametrisierung darstellen kann, wollen wir nicht nur den verhältnismäßig einfachen Algorithmus zur Zeichnung einer parametrisierten Kurve implementieren, sondern auch implizite Kurven zeichnen. Hierfür gibt es verschiedene Möglichkeiten, die mit zunehmenden Aufwand bessere Plots liefern. Ein paar Beispiele von Raumkurven:Beispiele
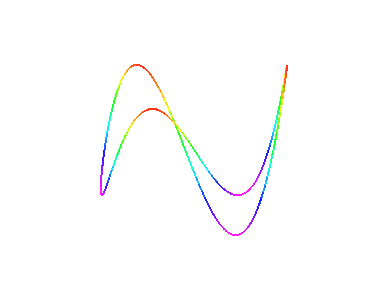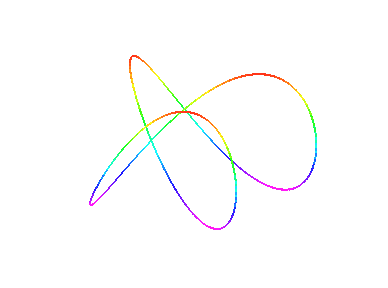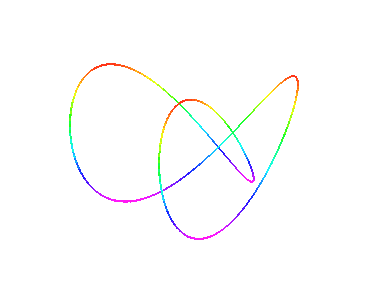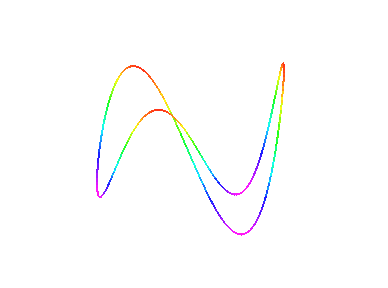
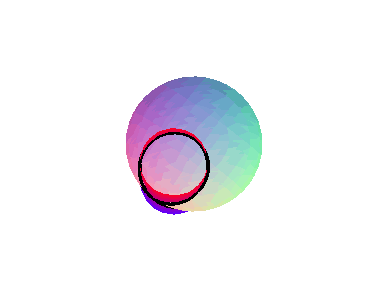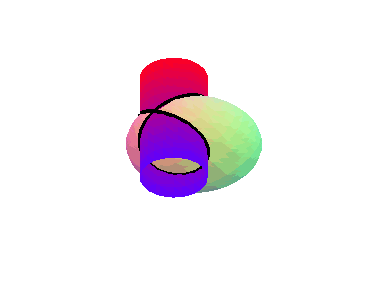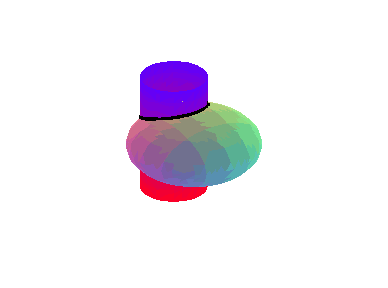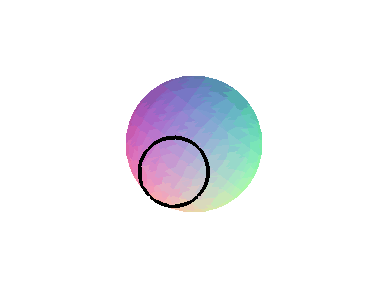
Wer einen 3D-Viewer und die entsprechende 3D-Brille hat, kann folgende Kurve 3-dimensional betrachten, oder man versucht die beiden Teilbilder schielend in der Mitte zu einem dritten zu verschmelzen:
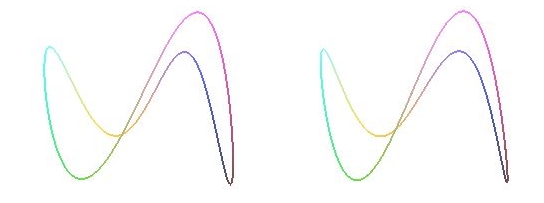

Betreuer
|
|
Dr. Timo v. Oertzen Zi. 427, Geb. 27 D-66123 Saarbrücken Tel. +49(0)681/302-3297 timovoe@gmx.de |
|
|
Janko
Böhm Zi. 428, Geb. 27 D-66123 Saarbrücken Tel. +49(0)681/302-2046 boehm@math.uni-sb.de |
![]()
 Hauptseite der Fachrichtung
Hauptseite der Fachrichtung
 Arbeitsgruppe Frank-Olaf Schreyer
Arbeitsgruppe Frank-Olaf Schreyer