Universität des Saarlandes Mathematik und Informatik AG Schreyer - Dr. Janko Böhm

Tel.: +49 (0)681/302-2046 boehm@math.uni-sb.de Zi. 425, Geb. E2 4 D-66123 Saarbrücken

Einführung in die Algebra und Zahlentheorie

Wintersemester 10/11

Ausblick: Auflösen von polynomialen Gleichungen durch Radikale

 Nicolo Tartaglia (1500-1557)           Girolamo Cardano (1501 - 1576)   

Sei f ein Polynom vom Grad d mit rationalen Koeffizienten.
Ist eine Darstellung der Nullstellen durch Radikale (d.h. ineinanderverschachtelte Wurzeln) stets möglich?

• Für Grad 2 gilt
  

• Für Grad 3 geht dies auch mit der Cardano-Formel von Nicolo Tartaglia (1500-1557):

  Wir können eine Gleichung vom Grad 3 stets auf die Form   bringen. Die Lösungen sind dann gegeben durch   wobei

• Auch für Grad 4 gibt es eine Formel von Ludovico Ferrari (1522-1565). Eine geometrische Methode die Formel herzuleiten finden Sie unten.

• Für Grad >4 ist dies i.A. nicht möglich, wie Abel gezeigt hat. Für welche speziellen Polynome es doch geht beantwortet die Galoistheorie.

Niels Abel (1802-1829)                   Evariste Galois (1811 - 1832)

Die Fragestellung der Auflösung von Polynomgleichungen durch Radikale wird behandelt in der Galoistheorie, in welcher Gruppen-, Ring- und Köpertheorie zusammenkommen. Die Grundidee ist folgende:
Da die Nullstellen a₁,...,a_d eines Polynoms f nicht eindeutig anordnen lassen, betrachtet man die Gruppe der Symmetrien Gal(f) der Menge der Nullstellen, genauer die Körperautomorphismen von Q[a₁,...,a_d ]. Die Gleichung f = 0 läßt sich durch Wurzeln auflösen genau dann, wenn die Galoisgruppe im Sinne der Gruppentheorie auflösbar ist.

Auflösen einer allgemeinen Gleichung 4. Grades durch Radikale

Mit einer linearen Transformation können wir ein Polynom 4. Grades auf die Form

x⁴ + b₂ · x² + b₁ · x + b₀

bringen. In der Grafik betrachten wir das Beispiel f  = x⁴ - 5 · x² + x + 4.

Statt f = 0 betrachten wir das Gleichungssystem

q₁= y - x² = 0

q₂ = y² + b₂ · y + b₁ · x + b₀ = 0

und suchen die 4 Schnittpunkte der Parabeln q₁ und q₂. Dazu betrachten wir die Schar von Quadriken

q₁ + t · q₂ = 0

mit dem Parameter t durch die 4 Schnittpunkte von q₁ und q₂

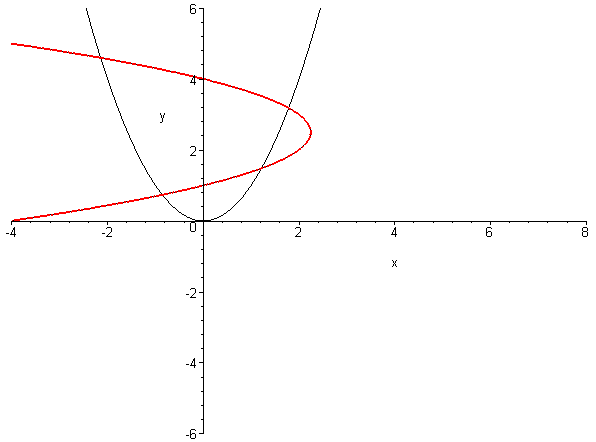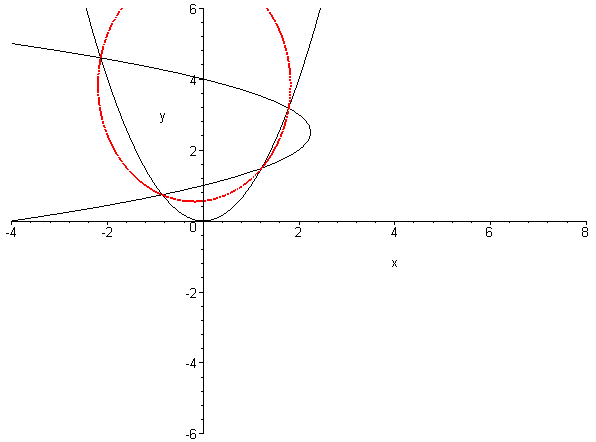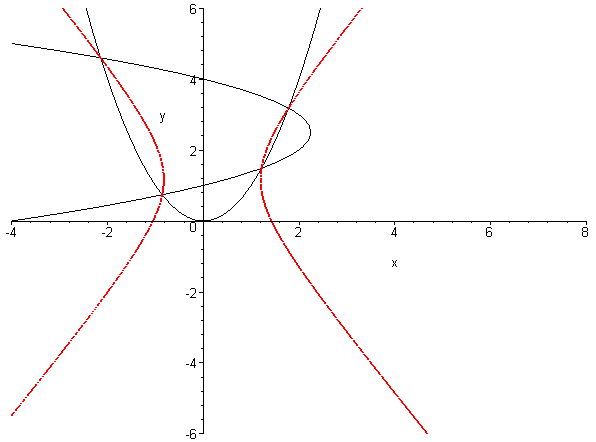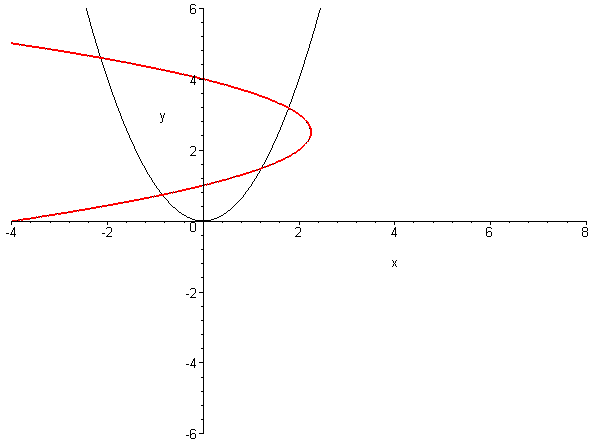
An 3 Werten für t wird die Konik q₁ + t · q₂ = 0 reduzibel, d.h. ist eine Vereinigung von 2 Geraden. Um diese Werte zu bestimmen schreiben wir die Quadrik in Matrixform:

q₁ + t · q₂ = (x,y,1)A(t)(x,y,1)^t

Die kubische Gleichung det(A(t)) = 0 heißt Resolvente von f und deren Nullstellen liefern die reduziblen Koniken.

Wählen wir nun einen solchen Wert t₀ aus:

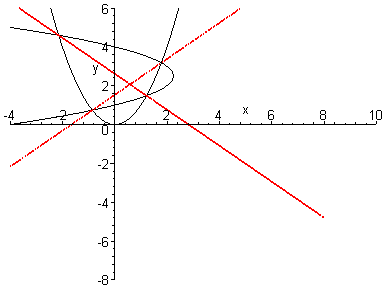
so können wir q₁ + t₀ · q₂ in Linearfaktoren faktorisieren als

q₁ + t₀ · q₂ = L₁ · L₂

durch Lösen einer quadratischen Gleichung.
Schließlich können wir einen Schnittpunkt von L₁ = 0 mit q₁ = y - x² durch Lösen einer weiteren quadratischen Gleichung bestimmen. In Formeln übersetzt erhalten wir so eine Darstellung der Nullstellen durch Radikale.

Die Wahlmöglichkeiten in den Formeln: 
2 · 3 um die kubische Resolvente zu lösen, die Wahl der Gerade, die Wahl des Schnittpunkts gibt insgesamt:

2³ · 3 = 24

Möglichkeiten. Für allgemeine Koeffizenten ist dies die Ordnung der Galoisgruppe.

Übung: Schreiben Sie die resultierende Formel auf!

  Hauptseite der Fachrichtung   Arbeitsgruppe Frank-Olaf Schreyer  Einführung in die Algebra und Zahlentheorie