-
g1 :
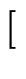 1, 11
1, 11![$ \left.\vphantom{ 1,11}\right]$](images/img2.gif)

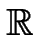
g1
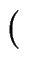 k
k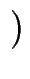 = L2^k
= L2^k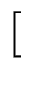
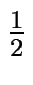 , 1
, 1![$ \left.\vphantom{ \frac{1}{2},1}\right]$](images/img9.gif)
-
g2 :
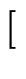 1, 11
1, 11![$ \left.\vphantom{ 1,11}\right]$](images/img2.gif)

g2
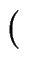 k
k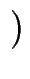 = L2^k
= L2^k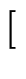 0, 4
0, 4![$ \left.\vphantom{ 0,4}\right]$](images/img11.gif)
-
g3 :
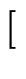 1, 11
1, 11![$ \left.\vphantom{ 1,11}\right]$](images/img2.gif)

g3
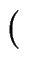 k
k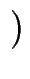 = L2^k
= L2^k 1,
1,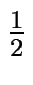
![$ \left.\vphantom{ 1,\frac{1}{2}}\right]$](images/img13.gif)
- 510511
- 5302555407858282827768779093
- 713623837172067545560252416065537
- 42144985531257745681402189153111135
- 12098743833798169067520000007523445343024140716896711111
- 64898518442585961302416669382254503060920596574980..
..25293841379902123372605065112731390344140051162106..
..64274752968417922051839654930184534182840779371249..
..77201178904854777462019451974017116414724852487815..
..1680000000000000001 - 2468001160766705452066353134549702698515108744549..
..4665685615343871770215418328461561352271369287472..
..2894942800453480535296312038337227963302750841644..
..8080849156722646366456990845503383352913528008289..
..3217698465676926977153625636105890357806909711920..
..3632383280760251916550382742710343646274895445668..
..7336461016448159044677999713509355259225543554112..
..189128101829876543546780098765000111111111200611
mit Probedivision, Pollards
![]() p - 1
p - 1![]() -Methode und mit dem
Quadratischen Sieb (soweit jeweils anwendbar).
-Methode und mit dem
Quadratischen Sieb (soweit jeweils anwendbar).
28940876200588807614880444715257804099176669707381..
..18342040725536981792071169315573271203611095429446..
..91101712755066527975565713841027366846493109170684
Der öffentliche Schlüssel ist:
n =3345252661316380710817006205344075166515200000000100..
0000000000000000000000000000000000000000000000893182..
4605714736497881406568268680694595584000000267
e =65537
Die Nachricht wurde im Alphabet
![]() A..Z
A..Z![]()
![]()
![]() /26
kodiert durch
/26
kodiert durch
| A | ||
| B | ||
| Y | ||
| Z |
und die dann erhaltene Zahl mit RSA verschlüsselt.