Kryptographie - Algebraischer Hintergrund
Prof . Dr. F.-O. Schreyer
Übungsblatt 3: Elliptische Kurven und Faktorisierung
Abgabetermin 21.5.2002
Voraussetzungen: Vorlesungskapitel Faktorisierung, Elliptische Kurven.
- Für q eine Primzahl. Schreiben Sie eine Maple-Prozedur, die die
Punke einer
elliptischen Kurve
a, b 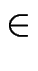
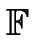 q bestimmt.
q bestimmt.
- Für q eine Primzahl. Schreiben Sie eine Maple-Prozedur, die die
Anzahl
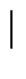 Ea, b
Ea, b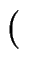
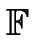 q
q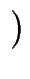
 der Punke der
elliptischen Kurve
Ea, b
der Punke der
elliptischen Kurve
Ea, b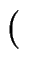
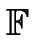 q
q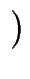 bestimmt
(Vergessen Sie den Punkt im Unendlichen nicht).
bestimmt
(Vergessen Sie den Punkt im Unendlichen nicht).
- Bestimmen Sie für alle Primzahlen
5
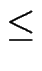 p
p 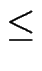 29 die Anzahl der
Punkte von
E
29 die Anzahl der
Punkte von
E
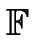 p
p : y2 = x3 + 1. Wann ist
: y2 = x3 + 1. Wann ist
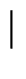 E
E
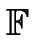 p
p
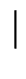 = p + 1 ?
= p + 1 ?
- Für q eine Primzahl. Schreiben Sie eine Maple-Prozedur, die
 Ea, b
Ea, b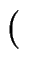
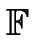 q
q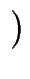
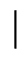 für alle
a, b
für alle
a, b 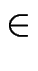
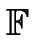 q bestimmt und damit den Satz von Hasse verifiziert.
q bestimmt und damit den Satz von Hasse verifiziert.
- Schreiben Sie eine Maple-Prozedur, die P + Q für zwei Punkte P
und Q auf einer elliptischen Kurve
Ea, b
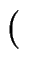
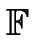 q
q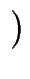 berechnet. Vergessen Sie den Fall P = Q und den Punkt O im Unendlichen nicht.
berechnet. Vergessen Sie den Fall P = Q und den Punkt O im Unendlichen nicht.
- Sei
t
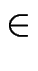
 und
P
und
P 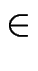 Ea, b
Ea, b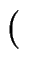
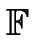 q
q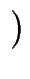 .
Schreiben Sie ein Maple-Skript, das t . P berechnet.
.
Schreiben Sie ein Maple-Skript, das t . P berechnet.
- Schreiben Sie ein Maple-Skript, das die
elliptische-Kurven-Faktorisierung wie in der Vorlesung beschrieben durchführt.
- Versuchen Sie die Zahlen aus dem Übungsblatt 2 mit Ihrem Skript zur
elliptischen-Kurven-Faktorisierung zu faktorisieren.
Abgabe der Aufgaben bitte als Maple-file per email an boehm@math.uni-sb.de.
janko
2002-05-10
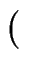
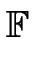 q
q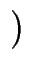 =
= 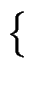
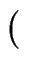 x, y
x, y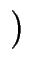
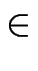
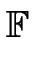 q2 | y2 = x3 + ax + b
q2 | y2 = x3 + ax + b
 O
O