Bob wählt eine Primzahl p und ein
g ![]()
![]() p * mit
p * mit
![]() p * =
p * = ![]() g
g![]() : =
: = ![]() gk | k = 0,..., p - 1
gk | k = 0,..., p - 1![]() .
.
Dann wählt er ein zufälliges
d ![]()
![]() 1,...p - 2
1,...p - 2![]() ,
welches er geheim hält.
,
welches er geheim hält.
Der öffentliche Schlüssel ist
gd ![]()
![]() p * zusammen
mit g und p.
p * zusammen
mit g und p.
Alice kann nun eine für Bob bestimmte Nachricht
T ![]()
![]() p * wie folgt verschlüsseln:
p * wie folgt verschlüsseln:
Alice wählt ein zufälliges
k ![]()
![]() 1,...p - 2
1,...p - 2![]() und
berechnet
und
berechnet
Kann man
d = logg![]() gd
gd![]() berechnen, dann hat man das System geknackt.
berechnen, dann hat man das System geknackt.
- Schreiben Sie eine Maple-Prozedur mit dem Alice eine Nachricht für
Bob mit dem ElGamal-Kryptosystem verschlüsseln kann.
- Schreiben Sie eine Maple-Prozedur mit der Bob diese Nachricht wieder
entschlüsseln kann.
- Schreiben Sie eine Maple-Prozedur, die das ElGamal-Kryptosystem knackt,
indem sie aus dem öffentlichen Schlüssel den geheimen Schlüssel berechnet.
- Probieren Sie Ihre Skripte mit einem frei gewählten Beispiel aus.
Bem: Das Kodieren und Dekodieren der Nachricht als Zahl soll wie im RSA Skript durchgeführt werden.
Bob wählt eine Primzahl p und eine elliptische Kurve
E![]()
![]() p
p![]() über
über
![]() p und einen Punkt
g
p und einen Punkt
g ![]() E
E![]()
![]() p
p![]() .
.
Sei
H : = ![]() g
g![]() die von g erzeugte zyklische
Untergruppe von
E
die von g erzeugte zyklische
Untergruppe von
E![]()
![]() p
p![]() .
.
Dann wählt er ein zufälliges
d ![]()
![]() 1,...
1,...![]() H
H![]() - 1
- 1![]() , welches er geheim hält.
, welches er geheim hält.
Der öffentliche Schlüssel ist d . g zusammen mit g und
E![]()
![]() p
p![]() .
.
Alice kann nun eine für Bob bestimmte Nachricht
T ![]() E
E![]()
![]() p
p![]() wie folgt verschlüsseln:
wie folgt verschlüsseln:
Alice wählt ein zufälliges
k ![]()
![]() 1,...
1,...![]() H
H![]() - 1
- 1![]() und berechnet
und berechnet
- Schreiben Sie eine Maple-Prozedur, mit der Alice eine Nachricht für
Bob mit dem elliptischen Kurven ElGamal Kryptosystem verschlüsseln kann.
- Schreiben Sie eine Maple-Prozedur, mit der Bob diese Nachricht wieder
entschlüsseln kann.
- Probieren Sie Ihr Skript mit der elliptischen Kurve
E : y2 = x3 + x + 1
über
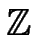 /5
/5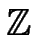 mit einem beliebigen Punkt g und einem
Punkt der Kurve als Nachricht aus.
mit einem beliebigen Punkt g und einem
Punkt der Kurve als Nachricht aus.
- Haben Sie eine Idee, wie man auf elliptischen Kurven den log berechnen und damit ElGamal knacken kann.