Bob wählt also 2 irreduzible Polynome g und h aus
![]() p
p![]() x
x![]() , berechnet
f = g . h und
, berechnet
f = g . h und
| = ord |
||
| = |
Dann wählt Bob ein zufälliges e mit
ggT![]() e,
e,![]()
![]() f
f![]()
![]() = 1 und bestimmt d mit
= 1 und bestimmt d mit
e . d 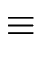 1mod
1mod
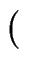 f
f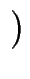
Bobs öffentlicher Schlüssel ist dann
Alice kann nun eine für Bob bestimmte Nachricht
m ![]()
![]() p
p![]() x
x![]() /
/![]() f
f![]() verschlüsseln (wobei m teilerfremd mit
f sei) mittels
verschlüsseln (wobei m teilerfremd mit
f sei) mittels
c : = memodf
Bob bekommt wieder den Klartext durch:
cd = md . e = m![$\scriptstyle ^{{%%
\begin{array}[c]{c}%%
{\tiny 1+k\cdot\varphi}\left( f\right)
\end{array}}}$](images/img37.gif) = mmodf
= mmodf
![$\scriptstyle ^{{%%
\begin{array}[c]{c}%%
{\tiny 1+k\cdot\varphi}\left( f\right)
\end{array}}}$](images/img37.gif) = mmodf
= mmodf
- Warum kann man dieses Kryptosystem leicht knacken ?
- Überprüfen Sie, daß dieses Kryptosystem auch deshalb zu
schwach ist, weil sich z.B. Polynome vom Grad
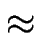 300 über
300 über
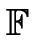 11 faktorisieren lassen.
11 faktorisieren lassen.
- Berechnen Sie per Hand:
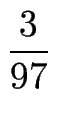
 ,
, 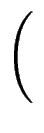
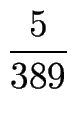
 ,
,
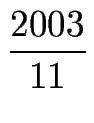
 ,
, 
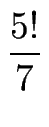
- Zeigen Sie
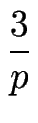
 =
= ![$\displaystyle \left\{\vphantom{
\begin{array}[c]{ll}%%
1 & \text{falls }p\equiv...
...2\text{ und}\\
-1 & \text{falls }p\equiv5,7\text{ mod }12
\end{array}}\right.$](images/img54.gif)
![$\displaystyle \begin{array}[c]{ll}%%
1 & \text{falls }p\equiv1,11\text{ mod }12\text{ und}\\
-1 & \text{falls }p\equiv5,7\text{ mod }12
\end{array}$](images/img55.gif)
![$\displaystyle \left.\vphantom{
\begin{array}[c]{ll}%%
1 & \text{falls }p\equiv1...
...\text{ und}\\
-1 & \text{falls }p\equiv5,7\text{ mod }12
\end{array}}\right\}$](images/img56.gif)
- Zeigen Sie direkt, daß
(Tip: Sei g eine primitive Wurzel von
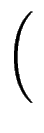
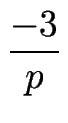
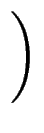 = 1 falls p
= 1 falls p  1mod3
1mod3
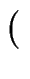
 /p
/p
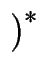 . Konstruieren Sie aus g ein Element h der Ordnung 3
und zeigen Sie, daß
. Konstruieren Sie aus g ein Element h der Ordnung 3
und zeigen Sie, daß
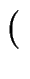 2 . h + 1
2 . h + 1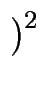
 -3modp).
-3modp).
![$\displaystyle \begin{array}[c]{c}%%
\text{boehm@btm8x5.mat.uni-bayreuth.de}\\ ...
...{\text{oder}}\\
\multicolumn{1}{l}{\text{boehm@math.uni-sb.de}}%%
\end{array}$](images/img65.gif)