Kryptographie - Algebraischer Hintergrund
Prof . Dr. F.-O. Schreyer
Übungsblatt 6: Der Hintergrund von Hasses Theorem
Abgabetermin 25.6.2002
Voraussetzungen: Vorlesungskapitel Endliche Körper, Hintergrund von Hasses Theorem.
- Schreiben Sie ein Maple-Skript, das über einem endlichen Körper
![$ \begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}$](images/img1.gif) die Anzahl Punkte
einer elliptischen Kurve
E : x3 + a . x + b - y2 = 0,
a, b
die Anzahl Punkte
einer elliptischen Kurve
E : x3 + a . x + b - y2 = 0,
a, b 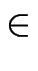
![$ \begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}$](images/img8.gif) zählt. Zum Rechnen in
zählt. Zum Rechnen in
![$ \begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}$](images/img9.gif) sind folgende Maple-Kommandos hilfreich (wenn Sie nicht Ihre Implementation
vom letzten Übungsblatt verwenden wollen oder diese noch nicht fertig ist)
sind folgende Maple-Kommandos hilfreich (wenn Sie nicht Ihre Implementation
vom letzten Übungsblatt verwenden wollen oder diese noch nicht fertig ist)
- Schreiben Sie ein Maple-Skript, das aus N1 die reziproken
Nullstellen
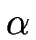 ,
,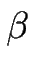 von
von
1 - at + pt2 bestimmt und
Nr = 1 +
pr -

-
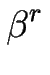
für festes N1 berechnet.
- Schreiben Sie ein Maple-Skript, das aus N1 mit der Weilformel
Nr berechnet, indem Sie für vorgegebenes r die
Potenzreihenentwicklung der logarithmischen Ableitung von
Z
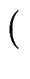 E/
E/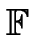 p, t
p, t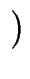 in t bis zur Ordnung r ausrechnen.
in t bis zur Ordnung r ausrechnen.
- Vergleichen Sie an Beispielen die Ergebnisse von Aufgabe 1, 2 und
3.
- Sei
f
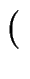 x, y
x, y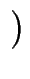 : =
xy
: =
xy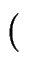 x2 - y2
x2 - y2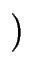 - 1 und
C die durch f = 0 definierte Kurve und
Nr : =
- 1 und
C die durch f = 0 definierte Kurve und
Nr : = ![$ \left\vert\vphantom{ \left\{ \left(
a,b\right) \in \begin{array}[c]{c}%%
\left...
...F}_{p^{r}}\right) ^{2}%%
\end{array}\mid f\left( a,b\right) =0\right\} }\right.$](images/img22.gif)
![$ \left\{\vphantom{ \left(
a,b\right) \in \begin{array}[c]{c}%%
\left( \mathbb{F}_{p^{r}}\right) ^{2}%%
\end{array}\mid f\left( a,b\right) =0}\right.$](images/img23.gif)
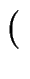 a, b
a, b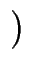
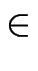
![$ \begin{array}[c]{c}%%
\left( \mathbb{F}_{p^{r}}\right) ^{2}%%
\end{array}$](images/img26.gif) | f
| f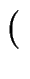 a, b
a, b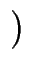 = 0
= 0![$ \left.\vphantom{ \left(
a,b\right) \in \begin{array}[c]{c}%%
\left( \mathbb{F}_{p^{r}}\right) ^{2}%%
\end{array}\mid f\left( a,b\right) =0}\right\}$](images/img27.gif)
![$ \left.\vphantom{ \left\{ \left(
a,b\right) \in \begin{array}[c]{c}%%
\left( \m...
...p^{r}}\right) ^{2}%%
\end{array}\mid f\left( a,b\right) =0\right\} }\right\vert$](images/img28.gif) + 4 die Anzahl der Punkte von
C über
+ 4 die Anzahl der Punkte von
C über
![$ \begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}$](images/img29.gif) (Bemerkung: Es gibt 4 Punkte im Unendlichen, da es 4 Asymptoten gibt).
Bestimmen Sie N1,...,N7 für p = 3 und stellen Sie eine Vermutung
für die Gestalt der Zetafunktion
auf, indem Sie
Z
(Bemerkung: Es gibt 4 Punkte im Unendlichen, da es 4 Asymptoten gibt).
Bestimmen Sie N1,...,N7 für p = 3 und stellen Sie eine Vermutung
für die Gestalt der Zetafunktion
auf, indem Sie
Z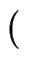 C/
C/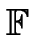 p;t
p;t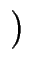 .
. 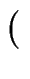 1 - t
1 - t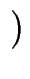 .
. 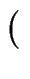 1 - pt
1 - pt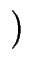 bis zur Ordnung 7 bestimmen.
bis zur Ordnung 7 bestimmen.
Welchen Betrag haben die reziproken Nullstellen (Maple-Kommandos solve und
abs)?
Abgabe der Aufgaben bitte als email an
janko
2002-06-25
![$\displaystyle \left\vert\vphantom{ E\left(
\begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}\right) }\right.$](images/img2.gif) E
E![$\displaystyle \left(\vphantom{
\begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}}\right.$](images/img3.gif)
![$\displaystyle \begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}$](images/img4.gif)
![$\displaystyle \left.\vphantom{
\begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}}\right)$](images/img5.gif)
![$\displaystyle \left.\vphantom{ E\left(
\begin{array}[c]{c}%%
\mathbb{F}_{p^{r}}%%
\end{array}\right) }\right\vert$](images/img6.gif)
![$\displaystyle \begin{array}[c]{l}%%
G:=GF\left( p,r\right) \text{ ist }\mathbb{...
...berechnet }a^{j}\\
G[\lq inverse\lq ](a)\text{ berechnet }\frac{1}{a}%%
\end{array}$](images/img10.gif)
 -
- 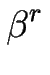
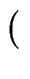 C/
C/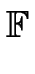 p;t
p;t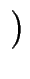 : = exp
: = exp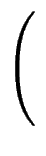
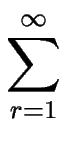 Nr
Nr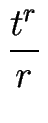
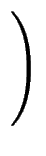
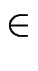
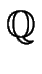
![$\displaystyle \left[\vphantom{ \left[ t\right] }\right.$](images/img39.gif)
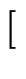 t
t![$\displaystyle \left.\vphantom{ t}\right]$](images/img41.gif)
![$\displaystyle \left.\vphantom{ \left[ t\right] }\right]$](images/img42.gif)
![$\displaystyle \begin{array}[c]{l}%%
\text{boehm@btm8x5.mat.uni-bayreuth.de}\\
\text{oder}\\
\text{boehm@math.uni-sb.de}%%
\end{array}$](images/img49.gif)