Kryptographie - Algebraischer Hintergrund
Prof . Dr. F.-O. Schreyer
Übungsblatt 7: Diskrete Logarithmen
Abgabetermin 2.7.2002
Voraussetzungen: Vorlesungskapitel Diskrete Logarithmen, Elliptische Kurven.
- Implementieren Sie Shanks' baby-step giant-step Methode zur Berechnung
von diskreten Logarithmen für eine allgemeine Gruppe G und testen Sie
Ihr Skript mit
-
G =
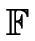 p * und
p * und
-
G = E

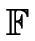 p
p . Bestimmen Sie nicht die
Gruppenordnung
. Bestimmen Sie nicht die
Gruppenordnung
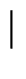 E
E
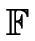 p
p
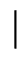 , sondern
verwenden Sie die obere Abschätzung aus dem Satz von Hasse.
, sondern
verwenden Sie die obere Abschätzung aus dem Satz von Hasse.
- Implementieren Sie Pollards
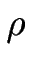 -Methode zur Berechnung von diskreten
Logarithmen in
-Methode zur Berechnung von diskreten
Logarithmen in
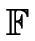 p * (Speicherung von
p * (Speicherung von
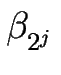 und
und
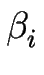 für
i = 2j +1,..., 2j+1) und testen Sie sie an Beispielen.
für
i = 2j +1,..., 2j+1) und testen Sie sie an Beispielen.
- Implementieren Sie den Pohlig-Hellman-Algorithmus für
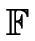 p * und testen Sie ihn
p * und testen Sie ihn
an Beispielen.
- Vergleichen Sie die Laufzeit der Skripte aus den Aufgaben 1, 2 und
3 an Beispielen.
- Berechnen Sie mit dem Index-Calculus-Algorithmus unter Verwendung der
Faktorbasis
F : =

2, 3, 5
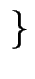
die Lösung von
13
x 
19mod479
Abgabe der Aufgaben bitte als email an:
janko
2002-06-26
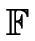 p * und
p * und

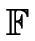 p
p . Bestimmen Sie nicht die
Gruppenordnung
. Bestimmen Sie nicht die
Gruppenordnung
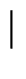 E
E
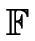 p
p
 , sondern
verwenden Sie die obere Abschätzung aus dem Satz von Hasse.
, sondern
verwenden Sie die obere Abschätzung aus dem Satz von Hasse.
 2, 3, 5
2, 3, 5
 19mod479
19mod479
![$\displaystyle \begin{array}[c]{l}%%
\text{boehm@btm8x5.mat.uni-bayreuth.de}\\
\text{oder}\\
\text{boehm@math.uni-sb.de}%%
\end{array}$](images/img12.gif)