




Next: Operator algebras
Up: Multiplicative Structures
Previous: Basic examples of operator
Contents
Index
Let
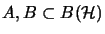 be
be 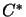 -algebras with
-algebras with
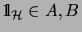 ,
and let
,
and let 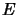 and
and 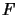 be two
be two
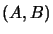 -operator modules, i.e. (algebraic)
-operator modules, i.e. (algebraic)
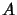 -left-
-left-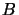 -right-modules.
A mapping
-right-modules.
A mapping
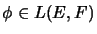 is called
is called 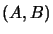 -module homomorphism (in case
-module homomorphism (in case 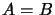
 -bimodule homomorphism) if
for all
-bimodule homomorphism) if
for all 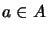 ,
,
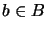 ,
, 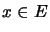 .
.
Furthermore we will write
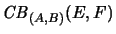 for the set of all completely bounded
for the set of all completely bounded 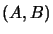 -module homomorphisms between
-module homomorphisms between 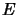 and
and 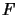 .
The space
.
The space
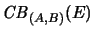 with the composition of operators as multiplication is a Banach algebra.
with the composition of operators as multiplication is a Banach algebra.
Let
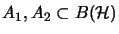 be
be 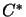 -algebras such that
-algebras such that
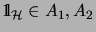 . Let further
. Let further
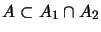 be a unital
be a unital
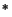 -subalgebra of
-subalgebra of 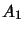 and
and 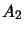 with
with
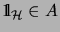 . An
. An 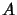 -bimodule homomorphism
-bimodule homomorphism
is called
self-adjoint if
for all 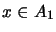 .
.
Dealing with completely bounded module homomorphisms, we have at our disposal a representation theorem,
an extension theorem and the following
decomposition theorem of Wittstock ([Wit81, Satz 4.5]
and cf. [Pau86, Thm. 7.5]):
Let 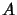 ,
, 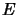 and
and 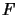 be unital
be unital 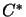 -algebras. Let moreover
-algebras. Let moreover 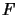 be
injective, and
be
injective, and 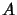 be a subalgebra of
be a subalgebra of 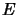 and
and 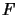 with
with
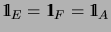 .
Then for each self-adjoint completely bounded
.
Then for each self-adjoint completely bounded 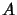 -bimodule homomorphism
-bimodule homomorphism
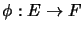 , there exist two completely positive
, there exist two completely positive 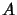 -bimodule homomorphisms
-bimodule homomorphisms 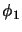 and
and 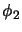 sharing the properties
sharing the properties
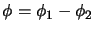 and
and
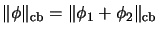 .
.
Consider two von Neumann algebras 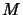 and
and 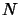 , and two
, and two 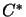 -algebras
-algebras
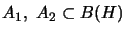 , where
, where
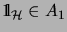 ,
, 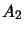 and
and
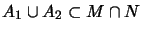 . We then have the
decomposition theorem of Tomiyama-Takesaki
(cf. [Tak79, Def. 2.15]):
Each operator
. We then have the
decomposition theorem of Tomiyama-Takesaki
(cf. [Tak79, Def. 2.15]):
Each operator
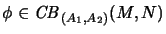 has a unique decomposition
has a unique decomposition
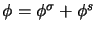 ,
,
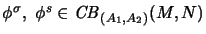 normal resp. singular, where
normal resp. singular, where
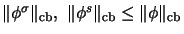 .
We thus obtain the algebraically direct sum decomposition:
.
We thus obtain the algebraically direct sum decomposition:
Here, the notions "normal" and "singular", repectively, are built in analogy to the framework of
linear functionals on a von Neumann algebra 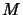 .24
.24
We list some basic facts about the spaces and mappings mentioned in (![[*]](crossref.png) ):
):
- (a)
- In case
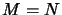 , all the spaces in (
, all the spaces in (![[*]](crossref.png) ) are Banach algebras.
) are Banach algebras.
- (b)
- The following properties of
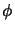 are hereditary for the normal part
are hereditary for the normal part
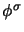 and
the singular part
and
the singular part 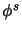 : completely positive, homomorphism,
: completely positive, homomorphism, 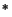 -homomorphism.
-homomorphism.
- (c)
- If
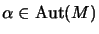 and
and
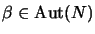 are
are 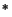 -automorphisms, we have
-automorphisms, we have
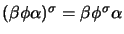 and
and
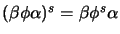 .
.
- (d)
- For
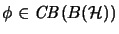 ,
,
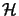 a Hilbert space, we have:
a Hilbert space, we have:
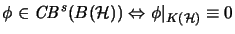 .
.
Let
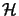 be a Hilbert space, and let
be a Hilbert space, and let
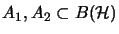 be two
be two 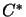 -algebras with
-algebras with
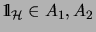 . Then we obtain
[Pet97, Prop. 4.2.5]:
. Then we obtain
[Pet97, Prop. 4.2.5]:
completely isometrically, where
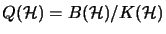 denotes the Calkin algebra.
denotes the Calkin algebra.
Let  be an arbitrary operator space. Then the space of all completely bounded
be an arbitrary operator space. Then the space of all completely bounded
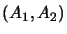 -module homomorphisms between
-module homomorphisms between  and
and
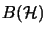 can be identified with
the dual of a
module Haagerup tensor product in the following way
([Pet97, p. 67], cf. also [ER91, Cor. 4.6],
[Ble92b, Prop. 2.3]):
can be identified with
the dual of a
module Haagerup tensor product in the following way
([Pet97, p. 67], cf. also [ER91, Cor. 4.6],
[Ble92b, Prop. 2.3]):
completely isometrically. Hence we see that
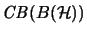 itself and (looking at (
itself and (looking at (![[*]](crossref.png) ), (
), (![[*]](crossref.png) )), just so,
)), just so,
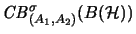 and
and
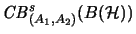 are dual operator spaces [Pet97, p. 70].
are dual operator spaces [Pet97, p. 70].
Footnotes
- ....24
- Let
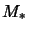 denote the (unique) predual of
denote the (unique) predual of 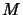 .
Then we have the
.
Then we have the 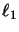 -direct sum decomposition
of
-direct sum decomposition
of 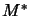 into normal (i.e.
into normal (i.e. 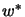 -continuous) and singular functionals.
[In the literature, one usually writes
-continuous) and singular functionals.
[In the literature, one usually writes
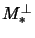 instead of
instead of 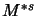 , corresponding to
, corresponding to
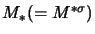 .]
Analogously, an operator
.]
Analogously, an operator
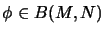 ,
, 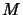 ,
, 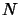 von Neumann algebras, is called normal (i.e.
von Neumann algebras, is called normal (i.e.
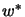 -
-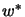 -continuous), if
-continuous), if
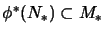 , and it is called singular, if
, and it is called singular, if
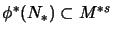 .
.





Next: Operator algebras
Up: Multiplicative Structures
Previous: Basic examples of operator
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() be
be ![]() -algebras such that
-algebras such that
![]() . Let further
. Let further
![]() be a unital
be a unital
![]() -subalgebra of
-subalgebra of ![]() and
and ![]() with
with
![]() . An
. An ![]() -bimodule homomorphism
-bimodule homomorphism
![]() ,
, ![]() and
and ![]() be unital
be unital ![]() -algebras. Let moreover
-algebras. Let moreover ![]() be
injective, and
be
injective, and ![]() be a subalgebra of
be a subalgebra of ![]() and
and ![]() with
with
![]() .
Then for each self-adjoint completely bounded
.
Then for each self-adjoint completely bounded ![]() -bimodule homomorphism
-bimodule homomorphism
![]() , there exist two completely positive
, there exist two completely positive ![]() -bimodule homomorphisms
-bimodule homomorphisms ![]() and
and ![]() sharing the properties
sharing the properties
![]() and
and
![]() .
.
![]() and
and ![]() , and two
, and two ![]() -algebras
-algebras
![]() , where
, where
![]() ,
, ![]() and
and
![]() . We then have the
decomposition theorem of Tomiyama-Takesaki
(cf. [Tak79, Def. 2.15]):
Each operator
. We then have the
decomposition theorem of Tomiyama-Takesaki
(cf. [Tak79, Def. 2.15]):
Each operator
![]() has a unique decomposition
has a unique decomposition
![]() ,
,
![]() normal resp. singular, where
normal resp. singular, where
![]() .
We thus obtain the algebraically direct sum decomposition:
.
We thus obtain the algebraically direct sum decomposition:
![[*]](crossref.png) ):
):
![[*]](crossref.png) ) are Banach algebras.
) are Banach algebras.
![]() be an arbitrary operator space. Then the space of all completely bounded
be an arbitrary operator space. Then the space of all completely bounded
![]() -module homomorphisms between
-module homomorphisms between ![]() and
and
![]() can be identified with
the dual of a
module Haagerup tensor product in the following way
([Pet97, p. 67], cf. also [ER91, Cor. 4.6],
[Ble92b, Prop. 2.3]):
can be identified with
the dual of a
module Haagerup tensor product in the following way
([Pet97, p. 67], cf. also [ER91, Cor. 4.6],
[Ble92b, Prop. 2.3]):
![[*]](crossref.png) ), (
), (![[*]](crossref.png) )), just so,
)), just so,