




Next: Convexity
Up: What are operator spaces?
Previous: Completely Bounded Multilinear Mappings
Contents
Index
Automatic Complete Boundedness
Completely bounded linear and multilinear mappings share
strong structural properties. Thanks to the complete boundedness
they have a very specific form
(cf. the corresponding representation theorems )
whence they are much more accessible than arbitrary bounded
linear (or multilinear) mappings.57
Moreover, even in the multilinear case we have at our disposal an
extension theorem
for completely bounded mappings -
which again is in striking contrast to the situation of arbitrary bounded (multi)linear mappings.
Because of the very nice structure theory
of completely bounded linear and multilinear mappings, respectively, it is highly interesting to
decide whether or not
a given bounded (multi)linear mapping actually is completely bounded.
The most elegant way to proceed is of course to check some simple conditions concerning the spaces involved and/or
some (purely) algebraic properties of the mapping which automatically imply the complete boundedness
of the latter.
In the following we shall collect various such criteria relying
- (1)
- on the initial and/or target space
- (2)
- mainly on algebraic properties of the mapping
(being, e.g., a
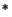 -homomorphism of
-homomorphism of
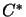 -algebras or a module homomorphism).
-algebras or a module homomorphism).
- (1)
- ``Criterion: spaces''
- (1.1)
- The linear case
-
Smith's lemma:
If
 is a matricially normed space and
is a matricially normed space and
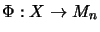 , where
, where
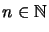 , is a
bounded linear operator, then we have
, is a
bounded linear operator, then we have
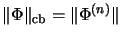 .
In particular,
.
In particular,
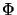 is completely bounded if and only if
is completely bounded if and only if
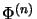 is bounded
[Smi83, Thm. 2.10].
is bounded
[Smi83, Thm. 2.10].
- Let
 be an operator space,
be an operator space,  a commutative
a commutative 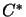 -algebra and
-algebra and
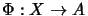 a bounded linear operator.
Then
a bounded linear operator.
Then 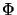 is completely bounded
and
is completely bounded
and
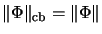 ([Loe75, Lemma 1], cf. also [Arv69, Prop. 1.2.2]).
([Loe75, Lemma 1], cf. also [Arv69, Prop. 1.2.2]).
In particular, every bounded linear functional
is automatically completely bounded
with the same cb-norm.
- The following theorem shows that, roughly speaking,
the above situations are the only ones
where every bounded linear operator between (arbitrary)
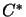 -algebras is automatically completely bounded. More precisely:
-algebras is automatically completely bounded. More precisely:
Let 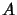 and
and 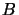 be
be 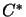 -algebras. In order to have the complete boundedness of very bounded linear operator from
-algebras. In order to have the complete boundedness of very bounded linear operator from 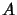 to
to
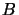 it is necessary and sufficient that either
it is necessary and sufficient that either 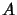 is finite dimensional
or
is finite dimensional
or 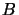 is a
subalgebra of
is a
subalgebra of
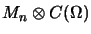 for a compact Hausdorff space
for a compact Hausdorff space 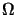 [HT83, Cor. 4], [Smi83, Thm. 2.8], cf. also [Smi83, p. 163].
[HT83, Cor. 4], [Smi83, Thm. 2.8], cf. also [Smi83, p. 163].
- (1.2)
- The bilinear case
- (2)
- ``Criterion: mappings''
- (2.1)
- The linear case
- Every
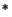 -homomorphism between
-homomorphism between 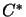 -algebras is
completely contractive.58
-algebras is
completely contractive.58
- Let
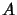 and
and 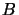 be
be 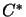 -subalgebras of
-subalgebras of 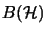 , where
, where 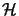 is a Hilbert space.
Let further
is a Hilbert space.
Let further
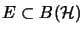 be an
be an 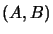 -operator module and
-operator module and
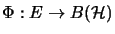 be a bounded
be a bounded 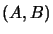 -module homomorphism.
Let
-module homomorphism.
Let
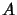 and
and 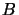 be
quasi-cyclic59, i.e., for every finite set of vectors
be
quasi-cyclic59, i.e., for every finite set of vectors
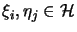 ,
,
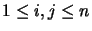 , there exist
, there exist
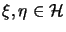 such that
such that
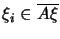 ,
,
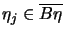 ,
,
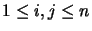 .
Then
.
Then 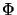 is completely bounded and
is completely bounded and
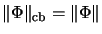 ([SS95, Thm. 1.6.1]; cf. also
[Smi91, Thm. 2.1] and [Smi91, Remark 2.2],
[Sat82, Satz 4.16]). - For special cases of this result obtained earlier see
[Haa80], [EK87, Thm. 2.5],
[PPS89, Cor. 3.3] and
[DP91, Thm. 2.4].
([SS95, Thm. 1.6.1]; cf. also
[Smi91, Thm. 2.1] and [Smi91, Remark 2.2],
[Sat82, Satz 4.16]). - For special cases of this result obtained earlier see
[Haa80], [EK87, Thm. 2.5],
[PPS89, Cor. 3.3] and
[DP91, Thm. 2.4].
- (2.2)
- The bilinear case
Footnotes
- ... mappings.57
- For example, the representation theorems provide a very useful tool
in calculating cohomology groups
(cf. for example the monograph [SS95]).
- ... contractive.58
- This is evident because
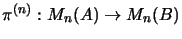 is a
is a
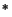 -homomorphism for every
-homomorphism for every
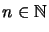 .
.
- ...quasi-cyclic59
- For example, cyclic
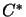 -algebras
are quasi-cyclic.
A von Neumann algebra
-algebras
are quasi-cyclic.
A von Neumann algebra 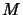 is quasi-cyclic if
every normal state on the commutant
is quasi-cyclic if
every normal state on the commutant 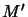 is a vector state
[Smi91, Lemma 2.3].
is a vector state
[Smi91, Lemma 2.3].





Next: Convexity
Up: What are operator spaces?
Previous: Completely Bounded Multilinear Mappings
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() and
and ![]() be
be ![]() -algebras. In order to have the complete boundedness of very bounded linear operator from
-algebras. In order to have the complete boundedness of very bounded linear operator from ![]() to
to
![]() it is necessary and sufficient that either
it is necessary and sufficient that either ![]() is finite dimensional
or
is finite dimensional
or ![]() is a
subalgebra of
is a
subalgebra of
![]() for a compact Hausdorff space
for a compact Hausdorff space ![]() [HT83, Cor. 4], [Smi83, Thm. 2.8], cf. also [Smi83, p. 163].
[HT83, Cor. 4], [Smi83, Thm. 2.8], cf. also [Smi83, p. 163].
![]() be a quasi-cyclic
be a quasi-cyclic
![]() -algebra and
-algebra and
![]() be an
be an ![]() -operator bimodule.
Let further
-operator bimodule.
Let further
![]() be a bilinear,
be a bilinear, ![]() -multimodular mapping such that
the corresponding linearization
-multimodular mapping such that
the corresponding linearization
![]() is bounded on
is bounded on
![]() .
.
![]() is completely bounded and
is completely bounded and
![]() [SS95, Thm. 1.6.2].
[SS95, Thm. 1.6.2].