



Next: Bipolar theorems
Up: Matrix convexity
Previous: Examples
Contents
Index
An important tool in the theory are the following separation theorems.
Let
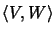 be a (non degenerate) duality of complex vector spaces. Thus
be a (non degenerate) duality of complex vector spaces. Thus
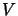 and
and 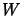 have weak topologies, and the matrix levels have the corresponding product
topology. For
have weak topologies, and the matrix levels have the corresponding product
topology. For
![$ v=[v_{i,j}]\in M_n(V)$](img1099.png) and
and
![$ w=[w_{k,l}]\in M_m(W)$](img1100.png) ,
,
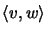 is defined by the joint amplifications of the duality:
is defined by the joint amplifications of the duality:
![$\displaystyle \langle v,w\rangle=[\langle v_{i,j},w_{k,l}\rangle]_{(i,k),(j,l)}$](img1102.png)
.
Note that the matrices, ordered by the cone of the positive semidefinite matrices, are
not totally ordered;
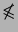 does not imply
does not imply 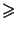 .
.
Theorem:62Let
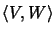 be a duality of complex vector spaces,
be a duality of complex vector spaces, 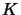 a closed set of
matrices over
a closed set of
matrices over 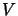 and
and
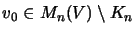 for some
for some 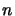 .
.
- a)
- [WW99, Thm. 1.6] If
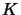 is matrix convex, then there
are
is matrix convex, then there
are
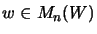 and
and
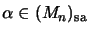 such that for all
such that for all
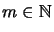 and
and 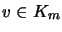
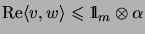
, but
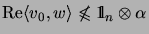
.
- b)
- [EW97b, Thm. 5.4] If
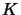 is matrix convex and
is matrix convex and 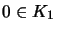 ,
then there is
,
then there is
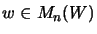 such that for all
such that for all
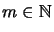 and
and 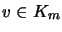
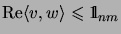
, but
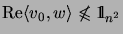
.
- c)
- [Bet97, p. 57] If
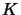 is a matrix cone, then there is
is a matrix cone, then there is
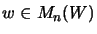 sucht that for all
sucht that for all
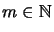 and
and 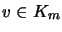
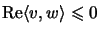
, but
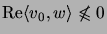
.
- d)
- [EW97a, Thm. 4.1] If
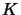 is absolutely matrix convex,
then tere is
is absolutely matrix convex,
then tere is
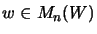 such that for all
such that for all
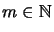 and
and 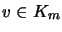
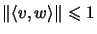
, but
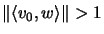
.
One can prove Ruan's theorem using the separation theorem for
absolutely matrix convex sets, applied to the unit ball of a matricially normed
space .
If 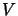 is a complex involutive vector space, one can find selfadjoint separating
functionals:
is a complex involutive vector space, one can find selfadjoint separating
functionals:
Theorem: 63Let
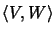 be a duality of complex involutive vector spaces,
be a duality of complex involutive vector spaces, 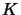 a closed
set of selfadjoint matrices over
a closed
set of selfadjoint matrices over 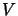 and
and
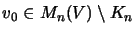 for some
for some
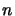 .
.
- b)
- If
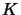 is matrix convex and
is matrix convex and 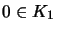 ,
then there is a
,
then there is a
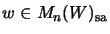 such that for all
such that for all
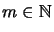 and
and 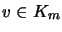
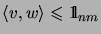
, but
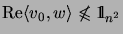
.
Footnotes
- ...Theorem:62
-
From this theorem one can easily get the following sharper version of the parts a), b)
and d):
- a)
- If
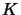 is matrix convex, then there are
is matrix convex, then there are
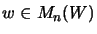 ,
,
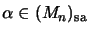 and
and
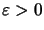 such that for all
such that for all
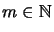 and
and 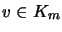
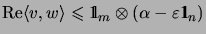
, but
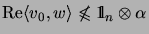
.
- b)
- If
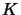 is matrix convex and
is matrix convex and 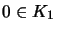 , then there are
, then there are
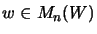 and
and
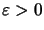 such that for all
such that for all
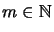 and
and 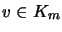
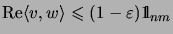
, but
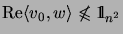
.
- d)
- If
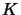 is absolutely matrix convex, then there are
is absolutely matrix convex, then there are
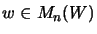 and
and
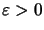 such that for all
such that for all
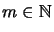 and
and 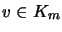
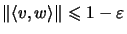
, but
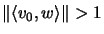
.
- ... 63
-
This theorem can be obtained from the above separation theorem, part a) and b). Note
that for selfadjoint
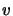 , the mapping
, the mapping
 is selfadjoint.
is selfadjoint.




Next: Bipolar theorems
Up: Matrix convexity
Previous: Examples
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() be a (non degenerate) duality of complex vector spaces. Thus
be a (non degenerate) duality of complex vector spaces. Thus
![]() and
and ![]() have weak topologies, and the matrix levels have the corresponding product
topology. For
have weak topologies, and the matrix levels have the corresponding product
topology. For
![]() and
and
![]() ,
,
![]() is defined by the joint amplifications of the duality:
is defined by the joint amplifications of the duality:
![]() does not imply
does not imply ![]() .
.
![]() be a duality of complex vector spaces,
be a duality of complex vector spaces, ![]() a closed set of
matrices over
a closed set of
matrices over ![]() and
and
![]() for some
for some ![]() .
.
![]() is a complex involutive vector space, one can find selfadjoint separating
functionals:
is a complex involutive vector space, one can find selfadjoint separating
functionals:
![]() be a duality of complex involutive vector spaces,
be a duality of complex involutive vector spaces, ![]() a closed
set of selfadjoint matrices over
a closed
set of selfadjoint matrices over ![]() and
and
![]() for some
for some
![]() .
.