




Next: Completely integral mappings
Up: Mapping Spaces
Previous: Mapping Spaces
Contents
Index
Let  and
and 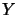 be operator spaces.
The
completely nuclear mappings
from
be operator spaces.
The
completely nuclear mappings
from  to
to 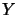 [ER94, §2], [EJR98, §3]
are defined by the
projective operator space tensor norm.
We consider the extension of the canonical identity
[ER94, §2], [EJR98, §3]
are defined by the
projective operator space tensor norm.
We consider the extension of the canonical identity
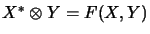 :
:
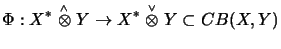
.

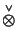 is the injective tensor product
and
is the injective tensor product
and
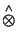 the projective tensor product .
the projective tensor product .
A mapping in the range of 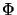 is called completely nuclear.
One denotes by
is called completely nuclear.
One denotes by
the space of the completely nuclear mappings and endows it with the
quotient operator space structure.
The operator space norm is denoted by
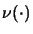 .
.
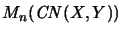 and
and
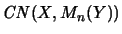 are in general not isometric.
are in general not isometric.
Nuclear 68
mappings are completely nuclear.
[ER94, 3.10]
In general, the projective tensor norm does not respect complete
isometries.
Hence,even for subspaces
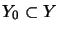 the canonical embedding
the canonical embedding
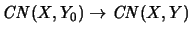 is generally
only completely contractive and not isometric.
Since the projective tensor norm respects quotient mappings,
every nuclear map
is generally
only completely contractive and not isometric.
Since the projective tensor norm respects quotient mappings,
every nuclear map
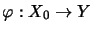 on a subspace
on a subspace
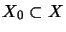 with
with
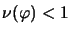 has an extension
has an extension
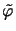 to the whole of
to the whole of  satisfying
satisfying
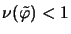 .
.
The completely nuclear mappings enjoy the
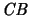 -ideal property .
Furthermore, the adjoint
-ideal property .
Furthermore, the adjoint 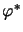 is
completely nuclear if
is
completely nuclear if 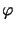 is, and the inequality:
is, and the inequality:
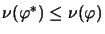 [EJR98, Lemma 3.2]
holds.
[EJR98, Lemma 3.2]
holds.
A mapping 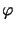 is completely nuclear, if and only if
there is a factorization of the form
is completely nuclear, if and only if
there is a factorization of the form
Here 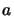 ,
, 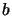 are Hilbert-Schmidt operators defining the
mapping
are Hilbert-Schmidt operators defining the
mapping
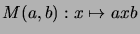 .
For the completely nuclear norm we have:
.
For the completely nuclear norm we have:
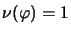 precisely
if for all
precisely
if for all
 there exists a factorization with
there exists a factorization with
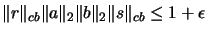 69 [ER94, Thm. 2.1].
69 [ER94, Thm. 2.1].
The completely nuclear mappings
are not local .
Footnotes
- ...Nuclear 68
- The completely nuclear mappings owe their definition
to the one of the nuclear mappings of
the Banach space theory.
There, one considers a corresponding mapping
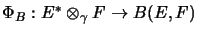 for two Banach spaces
for two Banach spaces 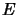 and
and 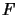 .
.
- ...
69
- In the Banach space theory one has an analogous statement:
A mapping
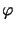 is nuclear, if and only if there's a diagram
is nuclear, if and only if there's a diagram
where 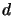 is a diagonal operator, i.e. , there is a
is a diagonal operator, i.e. , there is a
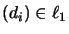 , such that
, such that
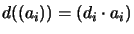 for all
for all
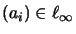 .
The nuclear norm is then computed as:
.
The nuclear norm is then computed as:
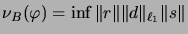 ,
where the infimum runs over all possible factorizations.
,
where the infimum runs over all possible factorizations.





Next: Completely integral mappings
Up: Mapping Spaces
Previous: Mapping Spaces
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![]() is called completely nuclear.
One denotes by
is called completely nuclear.
One denotes by
![]() the canonical embedding
the canonical embedding
![]() is generally
only completely contractive and not isometric.
Since the projective tensor norm respects quotient mappings,
every nuclear map
is generally
only completely contractive and not isometric.
Since the projective tensor norm respects quotient mappings,
every nuclear map
![]() on a subspace
on a subspace
![]() with
with
![]() has an extension
has an extension
![]() to the whole of
to the whole of ![]() satisfying
satisfying
![]() .
.
![]() -ideal property .
Furthermore, the adjoint
-ideal property .
Furthermore, the adjoint ![]() is
completely nuclear if
is
completely nuclear if ![]() is, and the inequality:
is, and the inequality:
![]() [EJR98, Lemma 3.2]
holds.
[EJR98, Lemma 3.2]
holds.
![]() is completely nuclear, if and only if
there is a factorization of the form
is completely nuclear, if and only if
there is a factorization of the form