



Next: Tensor matrix multiplication
Up: Tensor products
Previous: Tensor products of operator
Contents
Index
Joint amplification of a duality
The
matrix dualitywhich is fundamental in the duality theory of operator spaces,
is a special case of the
joint amplification
of a bilinear mapping.
The joint amplification of a duality
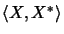 of vector spaces is defined by
for
of vector spaces is defined by
for
![$ x = [x_{ij}] \in M_p(X)$](img1329.png) ,
,
![$ \varphi = [\varphi_{\kappa\lambda}] \in M_q(X^*)$](img1330.png) .
Interpreting
.
Interpreting 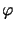 as a mapping
as a mapping
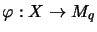 we have
Associated to the
duality
of tensor products74
we have
Associated to the
duality
of tensor products74
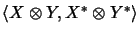 is the joint amplification
Especially, the equation
is the joint amplification
Especially, the equation
obtains, where
![$ x = [x_{ij}] \in M_{p_1}(X)$](img1338.png) ,
,
![$ y = [y_{kl}] \in M_{p_2}(Y)$](img1339.png) ,
,
![$ \varphi = [\varphi_{\kappa\lambda}] \in M_{q_1}(X^*)$](img1340.png) ,
,
![$ \psi = [\psi_{\mu\nu}] \in M_{q_2}(Y^*)$](img1341.png) .
.
Footnotes
- ... products74
- The duality
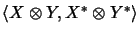 is defined by
is defined by
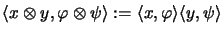 for
for
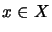 ,
, 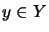 ,
,
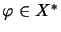 ,
,
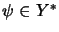 .
.
Prof. Gerd Wittstock
2001-01-07