Topological Recursion

Description:

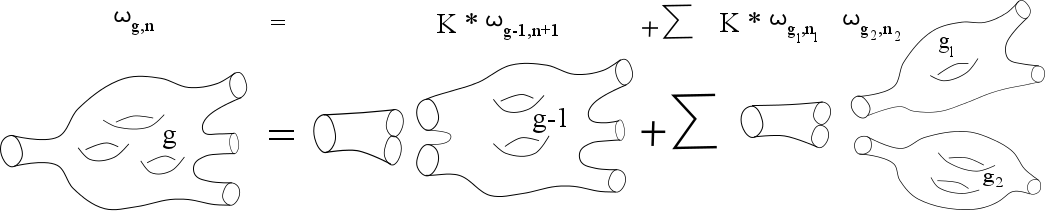
The topological recursion is a recursive fomula which computes a family of differential forms associated to given a spectral curve. It turns out these forms admit nice mathematical properties and compute interesting quantities in various field of mathematics. To mention some relations, the topological recursion computes

• Correlations functions in Random Matrix Theory,
• Hurwitz numbers in Enumerative Geometry.
• Gromov-Witten invariants and intersection numbers

The aim of the summer school is to give a introduction into the topic of topological recursion and highlight some recent developments.

The school is organized as follows. There will be lectures and tutorials held by leading experts. Moreover we will also cover a computational part, with an introductionary class on the use of the computer algebra system GAP for various types of factorization problems in the symmetric group (like different versions of Hurwitz numbers).

Invited Speakers

• Gaetan Borot, Max Planck Institute for Mathematics, Bonn
• Thomas Breuer, RWTH-Aachen University
• Olivia Dumitrescu, Central Michigan University
• Maksim Karev St. Petersburg Department of V.A. Steklov Institute of Mathematics
• Motohico Mulase, University of California, Davis

Location

The summer school will take place in:

• Campus Morgenstelle, Building C, Room N14 (entrance floor).

The campus is most conveniently reached by bus, the bus stop is called “BG Unfallklinik”. You can use the bus lines:

• 5, 13, 18 and 19 from the train station,
  
• 13, 18 and 19 from bus stop “Parkhaus König” or “Rümelinstraße” (which are close to the old town).

Activities

TBA

Organizers

• Christoph Goldner, Tübingen University
• Marvin Hahn, Tübingen University
• Felix Leid, Saarland University
• Hannah Markwig, Tübingen University
• Roland Speicher, Saarland University

License:

The picture “Schematic illustration of the topological recursion” above is taken from Wikipedia and is licensed by CC BY-SA 4.0 de , by “Eynard”.