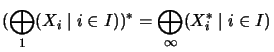Next: -direct sums
Up: Direct sums
Previous: -direct sums
Contents
Index
Let 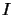 be an index set and
be an index set and  for each
for each  an operator space. Then there are an
operator space
an operator space. Then there are an
operator space  and complete contractions
and complete contractions
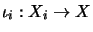 with the following
universal mapping property: For each family of complete contractions
with the following
universal mapping property: For each family of complete contractions
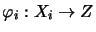 there is exactly one complete contraction
there is exactly one complete contraction
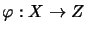 such that
such that
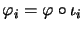 for all
for all 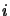 .
.
 is called
is called 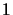 -direct sum of the
-direct sum of the 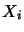 and is denoted by
and is denoted by
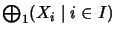 .The
.The 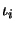 are completely isometric.
are completely isometric.
One can construct a 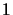 -direct sum for instance as the closure of the sums of the
images of the mappings
-direct sum for instance as the closure of the sums of the
images of the mappings
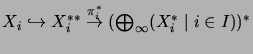 , where
, where 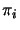 is the projection from
is the projection from
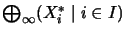 onto
onto 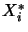 .
.
The equation
holds isometrically.
Prof. Gerd Wittstock
2001-01-07
![]() -direct sum for instance as the closure of the sums of the
images of the mappings
-direct sum for instance as the closure of the sums of the
images of the mappings
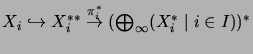 , where
, where ![]() is the projection from
is the projection from
![]() onto
onto ![]() .
.