Operator modules

Let $A_1, A_2 \subset B({\mathcal{H}})$ be $C^*$-algebras with $\mathrm{1\!\!\!\:l}_{{\mathcal{H}}} \in A_1, A_2$. A closed subspace $X$ of $B({\mathcal{H}})$ is called a concrete $(A_1,A_2)$-operator module , if $A_1X \subset X$ and $XA_2 \subset X$. Whenever $A_1=A_2=A$, we call $X$ a concrete $A$-operator bimodule (cf. [ER88, p. 137]).

In analogy to the operator space or the operator algebra situation, there is an abstract characterization of operator modules (cf. [Pop00, Déf. 4.1]):
Consider, as above, two unital $C^*$-algebras $A_1, A_2 \subset B({\mathcal{H}})$ with $\mathrm{1\!\!\!\:l}_{{\mathcal{H}}} \in A_1, A_2$, and an (algebraic) $(A_1,A_2)$-module $X$. We call $X$ an abstract $(A_1,A_2)$-operator module, if it carries an operator space structure satisfying the following axioms (of Ruan type):

(R1)	$\Vert axb\Vert _m$	$\leq$	$\Vert a\Vert \Vert x\Vert _m \Vert b\Vert$
(R2)	$\left\Vert \left( \begin{array}{cc} x & 0 \\ 0 & y \end{array} \right) \right\Vert _{m+n}$	$=$	${\rm {max}} \{ \Vert x\Vert _m, \Vert y\Vert _n \},$

where $m,n \in {\mathbb{N}}$, $a \in M_m(A_1)$, $x \in M_m(X)$, $y\in M_n(Y)$, $b \in M_m(A_2)$.

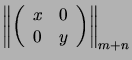For abstract operator modules holds a representation theorem of Ruan type (cf. [Pop00, Thm. 4.7]):
Let $V$ be an abstract $(A_1,A_2)$-operator module. Then there exist a Hilbert space $\mathcal{K}$, a complete isometry $\Theta: X \hookrightarrow B(\mathcal{K})$ and $^*$-representations $\pi_1$, $\pi_2$ of $A_1$ resp. $A_2$ in $B(\mathcal{K})$ such that:

$$\Theta(axb) = \pi_1(a) \Theta(x) \pi_2(b),$$

where $x \in X$, $a \in A_1$, $b \in A_2$. In case $A_1=A_2$, one can even choose $\pi_1=\pi_2$.