



Next: Examples
Up: Module tensor products
Previous: Module tensor products
Contents
Index
Let 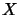 be a right operator module over a
be a right operator module over a 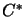 -algebra
-algebra 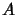 ,
,
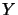 a left
a left 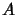 -operator module, and
-operator module, and 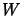 an operator space.
A bilinear mapping
an operator space.
A bilinear mapping
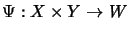 is called
balanced,
if the equation
obtains for all
is called
balanced,
if the equation
obtains for all
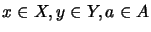 .
The module Haagerup tensor product is defined to be the
operator space
.
The module Haagerup tensor product is defined to be the
operator space
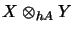 (which is unique up to complete isometry) together with a
bilinear, completely contractive,
balanced mapping
such that the following holds true:
For each bilinear, completely bounded balanced map
there is a unique linear
completely bounded
map
satisfying
(which is unique up to complete isometry) together with a
bilinear, completely contractive,
balanced mapping
such that the following holds true:
For each bilinear, completely bounded balanced map
there is a unique linear
completely bounded
map
satisfying
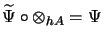 and
and
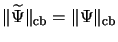 .
The module Haagerup tensor product can be realized in different ways:
.
The module Haagerup tensor product can be realized in different ways:
- Let
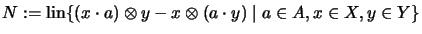
.
The
quotient space
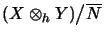 with its canonical matrix norms is an
operator space which satisfies the defintion
of
with its canonical matrix norms is an
operator space which satisfies the defintion
of
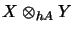 [BMP].
[BMP].
- Let us denote by
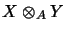 the algebraic module tensor product,
i.e. the quotient space
the algebraic module tensor product,
i.e. the quotient space
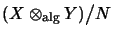 . For
. For
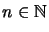 and
and
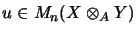 , by
we define a semi-norm
on
, by
we define a semi-norm
on
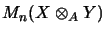 .
We obtain
and the semi-norms
.
We obtain
and the semi-norms
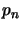 give an operator space norm on
give an operator space norm on
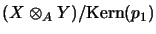 [Rua89].
The completion of this space satisfies the definition of
[Rua89].
The completion of this space satisfies the definition of
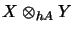 [BMP].
[BMP].




Next: Examples
Up: Module tensor products
Previous: Module tensor products
Contents
Index
Prof. Gerd Wittstock
2001-01-07
![$\displaystyle p_n(u) := \inf \left \{ \Vert S\Vert \Vert T\Vert \left\vert
u =...
...ght ],
l \in {\mathbb{N}}, S \in M_{nl}(X), T \in M_{ln}(Y) \right. \right\}
$](img966.png)