Let ![]() be a unital
be a unital ![]() -algebra.
A subset
-algebra.
A subset
![]() is a
is a ![]() -convex set, if
-convex set, if
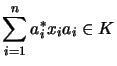
A subset
![]() is a
is a ![]() -absolutely convex set, if
-absolutely convex set, if
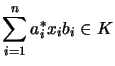
In particular ![]() -convex sets are convex and
-convex sets are convex and ![]() -absolutely convex sets are absolutely convex.
-absolutely convex sets are absolutely convex.
Example: Let ![]() be a Hilbert space and
be a Hilbert space and
![]() . The n-th matrix range of
. The n-th matrix range of ![]() is the set
is the set
The sets
Loebl and Paulsen introduced ![]() -convex sets in [LP81]. At the beginning of the nineties Farenick and Morenz studied
-convex sets in [LP81]. At the beginning of the nineties Farenick and Morenz studied ![]() -convex subsets of
-convex subsets of ![]() ([Far92],[FM93]). Eventually Morenz succeeded in proving an analogue of the Krein-Milman theorem for a compact
([Far92],[FM93]). Eventually Morenz succeeded in proving an analogue of the Krein-Milman theorem for a compact ![]() -convex subset of
-convex subset of ![]() ([Mor94]). At the end of the nineties Magajna generalized the notion of
([Mor94]). At the end of the nineties Magajna generalized the notion of ![]() -convex sets to the setting of operator modules and proved some separation theorems [Mag00, Th. 1.1] and also an analogue of the Krein-Milman theorem [Mag98, Th. 1.1].
-convex sets to the setting of operator modules and proved some separation theorems [Mag00, Th. 1.1] and also an analogue of the Krein-Milman theorem [Mag98, Th. 1.1].