3.1.4.1 Was ist ein Bruch?

Um den Weg zu beschreiben sollte man das Ziel kennen. Auf der Menge der geordneten Paare 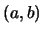$(a,b)$ natürlicher Zahlen, ist über

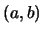$(a,b)$ steht in Relation zu 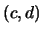$(c,d)$ genau dann, wenn 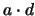$a\cdot d$ gleich 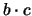$b\cdot c$ ist

eine Äquivalenzrelation erklärt. Die Bruchzahl bezeichnet die Äquivalenzklasse

$$\frac{m}{n}:=\{ (a,b) \; \vert \; a,b \in \mathbb{N}: m\cdot b=n\cdot a \}$$

Die Addition ist dann gemäß

$$\frac{m}{n}+\frac{p}{q} := \frac{m\cdot q+n\cdot p}{n \cdot q}$$

gegeben. Dies liegt jedoch etwas abseits der schulischen Wirklichkeit, knüpft nicht an Vorwissen der Schüler an. Besser sind folgende Ansätze:

• Eine Bruchzahl ist eine Größe. Bei diesem Konzept geht man von konkreten Brüchen aus. 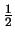$\frac{1}{2}$ Meter, 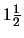$1\frac{1}{2}$ Stunden, 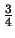$\frac{3}{4}$ Kuchen sind den Schülern aus dem täglichen Leben vertraut. Die Bruchzahl ist hier die Größe einer Einheit. Über diese Nähe zum täglichen Leben und die damit verbundenen Rückgriffsmöglichkeiten auf Vorkenntnisse der Schüler läßt sich die Addition über Anwendungssituationen anschaulich behandeln. Die Weg zur Multiplikation ist so allerdings verbaut.
• Bruchzahlen sind mathematische Operatoren. Hier wird zuerst die Multiplikation eingeführt: Die Bruchzahl als Abbildung eines Größenbereichs 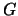$G$ in sich. Aus Veranschaulichungsgründen wählt man oft Längen, als Konkretisierung Maschinen die Stäbe zusammensetzen und teilen. Der Weg zur Addition führt über Erweitern, Kürzen, Gleichnamigmachen.