



Nächste Seite: 3.1.4.3 Endlich: Die Addition
Aufwärts: 3.1.4 Ein Beispiel kumulativen
Vorherige Seite: 3.1.4.1 Was ist ein
Inhalt
Index
Unterabschnitte
In der Regel findet die Bruchrechnung in der 6. Klasse statt.
Voraussetzung: Der Schüler kann mit natürlichen Zahlen rechnen.
Der Schüler sollte in die Lage versetzt werden verständig, nicht
rezepthaft, mit Bruchzahlen umzugehen. Dazu ist es sinnvoll die
zu erwerbenden Begriffe und Verfahren
aus ihren Umweltbezügen zu lösen.
Man kann verschiedene Anwendungsaspekte unterscheiden:
- Maßzahlaspekt (
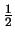 Meter)
Meter)
- Relationsaspekt (Die Erde ist zu
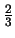 mit Wasser bedeckt)
mit Wasser bedeckt)
- Operatoraspekt (Nimm ein Viertel der Pizza)
- Quotientenaspekt (Die Karte ist im Maßstab 1:200000)
Der Maßzahlaspekt steht im Alltag im Vordergrund und bietet sich damit
als schulischer Zugang an.
Grundlage für die Einführung der Bruchzahlen ist Erfahrung im
Operieren mit konkreten Brüchen.
Hier muß man zwei Grundvorstellungen
unterscheiden:
- Bruch als Teil eines Ganzen
- oder mehrerer Ganzen.
Der erste Zugang ist einfacher zu realisieren. Konkrete Brüche
lassen sich durch Teilen eines vorgegebenen Streifens realisieren:
Durch wiederholtes halbierendes Falten wird durch Zweierpotenzen geteilt;
ein Papierstreifen wird gefünftelt durch zusammenrollen zu einem
geeigneten Querschnitt und zusammendrücken. Oder beliebige
Strecken lassen sich durch Einpassen in äquidistante Parallelen
(für den Schüler: Streifenmuster) in gleiche Teile zerlegen.
Diese Elementarbrüche können dann zusammengesetzt werden.
Die zweite Vorstellung sollte darauf aufbauen: Ein
Repräsentant der Länge 1 wird vervielfacht und dann geteilt.
Formal unterscheiden sich die Grundvorstellungen nur in der Reihenfolge
des Vervielfachens und Teilens. In realistischen Verteilungssituationen
- das Verteilen von drei Pizzas, die vielleicht noch nacheinander
auf den Tisch kommen, an vier Kinder -
scheint dies nicht selbstverständlich,
so daß der hier beschriebene
Weg des Aufeinanderaufbauens beschritten werden sollte. Abschließend ist
die Einsicht zu gewinnen, daß man in beiden Fällen zur selben
Lösung gelangt, für die man dann auch den selben
Namen verwenden darf.
Umgekehrt muß auch ein vorgegebener Repräsentant
durch einen und dann verschiedene konkrete Brüche benannt werden können.
In einfachen Fällen kann auch schon die Addition angesprochen werden.
(
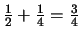 )
Nach einer gründlichen Beschäftigung mit konkreten
Brüchen kann die Abstraktion zu den Bruchzahlen erfolgen.
Der Schüler findet schnell:
)
Nach einer gründlichen Beschäftigung mit konkreten
Brüchen kann die Abstraktion zu den Bruchzahlen erfolgen.
Der Schüler findet schnell:
Gilt 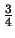 Meter
Meter 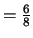 Meter so gilt auch
Meter so gilt auch
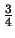 Pizza
Pizza 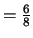 Pizza.
Pizza.
Gilt 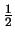 Kuchen
Kuchen
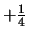 Kuchen
Kuchen 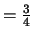 Kuchen so gilt dies auch für
Stunden.
Kuchen so gilt dies auch für
Stunden.
Schüler erkennen also:
Gilt eine Aussage für eine
Größeneinheit so gilt sie für alle.
Zur Bruchzahl gelangt man jetzt durch Weglassen der Einheit.
Die Brüche als Zahlen aufzufassen liegt nah:
- man kann damit rechnen,
- sie der Größe nach ordnen,
- sie auf dem Zahlenstrahl darstellen,
- mit
ihrer Hilfe Größen benennen.
Die Addition ungleichnamiger Brüche setzt einen weiteren Schritt voraus:
Erweitern und Kürzen.
Erweitern und Kürzen lassen sich an einem unterteilten Rechteck
veranschaulichen.
Die Verfeinerung der Unterteilung führt zum Erweitern,
die Vergröberung zum Kürzen. Erweitern ist beliebig möglich,
Kürzen nur bis zu einem Kernbruch.
Ist der Grundgedanke anschaulich verstanden - Übergang zu einem
anderen Namen für dieselbe Bruchzahl - und durch variierte
konkrete Beispiele vertieft, kann man die Regel formulieren:
Man erweitert bzw. kürzt einen Bruch, indem man Zähler und Nenner
mit derselben Zahl multipliziert, bzw. durch dieselbe Zahl dividiert.
Um das Kürzen zu optimieren benötigr man den Begriff des ggT.




Nächste Seite: 3.1.4.3 Endlich: Die Addition
Aufwärts: 3.1.4 Ein Beispiel kumulativen
Vorherige Seite: 3.1.4.1 Was ist ein
Inhalt
Index
Anselm Lambert
2001-05-25
Meter
Meter so gilt auch
Pizza
Pizza.
Kuchen
Kuchen
Kuchen so gilt dies auch für Stunden.