



Nächste Seite: 3.1.4.4 Lernhierarchien nach Gagne
Aufwärts: 3.1.4 Ein Beispiel kumulativen
Vorherige Seite: 3.1.4.2 Wie gelangt man
Inhalt
Index
Als Vorstufe zur Addition von Brüchen behandelt man Addition von Größen.
Diese läßt sich auf Repräsentantenebene leicht realisieren,
z.B. zeichnerisch oder durch zusammenschütten von Flüssigkeiten.
Dann kann man die Maßzahl bestimmen.
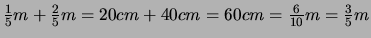 .
Bei diesen gleichnamigen Brüchen benötigt man nur die Gesamtzahl der
Teilstrecken (der Einheit
.
Bei diesen gleichnamigen Brüchen benötigt man nur die Gesamtzahl der
Teilstrecken (der Einheit 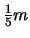 ) um die Maßzahl der Gesamtlänge
zu erhalten. Auf die Größeneinheit kommt es wieder nicht an.
Sind die betrachteten konkreten Brüche ungleichnamig, muß man
eine gemeinsame Unterteilung finden. Dies realisiert man z.B.
durch unterteilte Rechtecke: Zur Veranschaulichung von
) um die Maßzahl der Gesamtlänge
zu erhalten. Auf die Größeneinheit kommt es wieder nicht an.
Sind die betrachteten konkreten Brüche ungleichnamig, muß man
eine gemeinsame Unterteilung finden. Dies realisiert man z.B.
durch unterteilte Rechtecke: Zur Veranschaulichung von
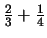 unterteilt man ein
Rechteck waagerecht dreimal und senkrecht viermal und erhält eine
Veranschaulichung der Größen (relativ zum Rechteck)
und eine gemeinsame Unterteilung. Dem Aufsuchen der gröbsten
gemeinsamen Unterteilung entspricht die Bestimmung des Hauptnenners.
Sind die konkreten Brüche dann gleichnamig addieren wir
die Zähler (die Größe) und behalten den Nenner (die Einheit) bei.
Dies kann als Regel formuliert werden.
Der hier beschriebene Weg entspricht dem abzuleitenden rechnerischen
Verfahren, die Additionsregel ist motiviert.
Der Schritt von den Größen zu den Bruchzahlen ist
unproblematisch: Bruchzahlen sind spezielle Größen.
unterteilt man ein
Rechteck waagerecht dreimal und senkrecht viermal und erhält eine
Veranschaulichung der Größen (relativ zum Rechteck)
und eine gemeinsame Unterteilung. Dem Aufsuchen der gröbsten
gemeinsamen Unterteilung entspricht die Bestimmung des Hauptnenners.
Sind die konkreten Brüche dann gleichnamig addieren wir
die Zähler (die Größe) und behalten den Nenner (die Einheit) bei.
Dies kann als Regel formuliert werden.
Der hier beschriebene Weg entspricht dem abzuleitenden rechnerischen
Verfahren, die Additionsregel ist motiviert.
Der Schritt von den Größen zu den Bruchzahlen ist
unproblematisch: Bruchzahlen sind spezielle Größen.




Nächste Seite: 3.1.4.4 Lernhierarchien nach Gagne
Aufwärts: 3.1.4 Ein Beispiel kumulativen
Vorherige Seite: 3.1.4.2 Wie gelangt man
Inhalt
Index
Anselm Lambert
2001-05-25