



Nächste Seite: Varianten des Induktionsprinzips
Aufwärts: Vollständige Induktion
Vorherige Seite: Summen und Produktzeichen
Inhalt
Induktionsprinzip
Wir setzen weiterhin die natürlichen Zahlen als bekannt voraus, wollen
aber ihre Eigenschafter etwas formaler beschreiben.
Das kann auf verschieden Weisen geschehen.
Üblich ist das folgende Axiomensystem (Peano Axiome), das wir hier nur
umgangssprachlich formulieren.
Die Axiome präzisieren den Vorgang des Zählens:
- Es gibt eine natürliche Zahl 1.
- Auf jede natürliche Zahl
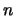 folgt eine nächste, die man mit
folgt eine nächste, die man mit
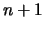 bezeichnet.
bezeichnet.
- Man kann beim Zählen nicht mehrmals auf dieselbe Zahl stoßen.
D.h. wenn zwei natürliche Zahlen
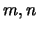 denselben Nachfolger haben,
sind sie gleich:
denselben Nachfolger haben,
sind sie gleich:
- Man kommt beim Zählen nicht zurück zur 1. D.h. für alle natürlichen
Zahlen
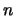 gil:
gil:
- Man erreicht durch Zählen, ausgehend von der 1, alle natürlichen
Zahlen.
Die zuletzt genannte Eigenschaft heißt das Induktionsprinzip.
Wir formulieren es in der Sprache der Mengenlehre.
Feststellung 1.2.6 (Induktionsprinzip)
Es sei
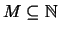
ein Teilmenge der natürlichen Zahlen
mit den Eigenschaften
- a)
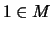
- b)
-
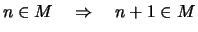
Dann folgt schon
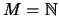
In den Anwendungen hat man eine Aussage 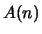 über eine
natürliche Zahlen
über eine
natürliche Zahlen 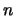 .
Die Aussage sei für alle natürlichen Zahlen formulierbar.
Man möchte die Aussage
.
Die Aussage sei für alle natürlichen Zahlen formulierbar.
Man möchte die Aussage 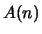 für jedes
für jedes
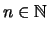 beweisen.
beweisen.
Dazu bilde man die Menge
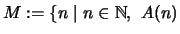
ist richtig für
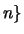
und zeige mit Hilfe des Induktionsprinzips, daß
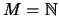 ist.
ist.
Dazu muß man für 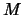 die Eigenschaften a) und b) nachweisen.
Man kommt so zu dem folgendem Beweisprinzip:
die Eigenschaften a) und b) nachweisen.
Man kommt so zu dem folgendem Beweisprinzip:
Feststellung 1.2.7 (Vollständige Induktion)
Für alle
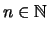 sei eine Aussage
sei eine Aussage 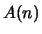 gegeben. Es gelte:
gegeben. Es gelte:
- Induktionsanfang:
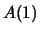 ist richtig .
ist richtig .
- Induktionsschritt:
- Für alle
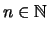 gilt der Schluß:
gilt der Schluß:
Dann ist
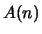
für alle
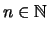
richtig.
Zum Beweis siehe
Vorlesung oder [KABALLO, S. 13].
Beispiele 1.2.8 (Induktionsbeweise)
.
- Dreiecksungleichung für endliche Reihen:
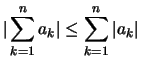
.

- Summenformel der geometrischen Reihe:
- Zweite binomische Formel:
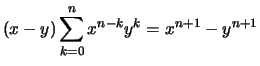
.

Zum Beweis siehe
Vorlesung oder [KABALLO, S. 14].




Nächste Seite: Varianten des Induktionsprinzips
Aufwärts: Vollständige Induktion
Vorherige Seite: Summen und Produktzeichen
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() über eine
natürliche Zahlen
über eine
natürliche Zahlen ![]() .
Die Aussage sei für alle natürlichen Zahlen formulierbar.
Man möchte die Aussage
.
Die Aussage sei für alle natürlichen Zahlen formulierbar.
Man möchte die Aussage ![]() für jedes
für jedes
![]() beweisen.
beweisen.
![]() die Eigenschaften a) und b) nachweisen.
Man kommt so zu dem folgendem Beweisprinzip:
die Eigenschaften a) und b) nachweisen.
Man kommt so zu dem folgendem Beweisprinzip:
![]() sei eine Aussage
sei eine Aussage ![]() gegeben. Es gelte:
gegeben. Es gelte: