



Nächste Seite: Fakultät, Binomialkoeffizient
Aufwärts: Vollständige Induktion
Vorherige Seite: Induktionsprinzip
Inhalt
Anmerkung. Aus den Peano-Axiomen folgen alle weiteren Eigenschaften
der natürlichen Zahlen; insbesondere:
- Die natürlichen Zahlen haben eine Anordnung (totale Ordnung).
- Die Addition und Multiplikation natürlicher Zahlen ergibt wieder
natürliche Zahlen.
Die Herleitung dieser Aussagen erfolgt in einer langen Kette an sich einfacher
Induktionsbeweise, die man aber in der richtigen Reihenfolge
durchführen muß (siehe [LANDAU] ).
Wir verwenden diese Regeln im folgenden kommentarlos.
Anmerkung. Darüber hinaus kann man zeigen:
- Jeder geordnete Körper, insbesondere
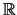 ,
enthält die natürlichen Zahlen.
,
enthält die natürlichen Zahlen.
Letzteres kann man auch zur Definition der natürlichen Zahlen erheben.
In einem strengen axiomatischen Aufbau führe man zunächst die reellen Zahlen
mit den folgenden Axiomen ein:
- Körperaxiome (K1)-(K11), Ordnung (O1)-(O3) und die Supremumseigenschaft (S)
Anschließend kann man die natürlichen Zahlen als
Teilmenge von
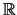 definieren und das Induktionsprinzip beweisen:
definieren und das Induktionsprinzip beweisen:
-
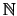 ist der Durchschnitt aller Teilmengen
ist der Durchschnitt aller Teilmengen
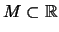 , die die folgenden
beiden Eigenschaften haben:
, die die folgenden
beiden Eigenschaften haben:
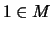 .
.
Aus 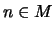 folgt
folgt 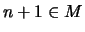 .
.
Es gibt solche Mengen 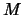 , z. B.
, z. B.
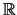 selber. Also ist
selber. Also ist
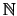 wohldefiniert und erfüllt das Induktionsprinzip.
wohldefiniert und erfüllt das Induktionsprinzip.
Manchmal ist es praktischer, eine Aussage nicht für die natürlichen Zahlen,
sondern für alle ganzen Zahlen ab einem
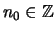 zu formulieren:
zu formulieren:
Feststellung 1.2.9 (Vollständige Induktion ab
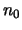
)
Es sei
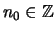 . Für
. Für
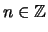 mit
mit
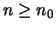 sei eine Aussage
sei eine Aussage 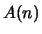 gegeben. Es gelte:
gegeben. Es gelte:
- Induktionsanfang:
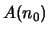 ist richtig .
ist richtig .
- Induktionsschritt:
- Für alle
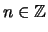 ,
, 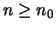 gilt der Schluß:
gilt der Schluß:
Dann ist
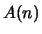
für alle
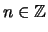
mit
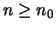
richtig.
Manchmal ist es hilfreich, statt der Aussage 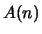 die folgende Aussage
zu beweisen:
die folgende Aussage
zu beweisen:
Beim Induktionschluß
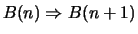 hat man stärkere
Vorraussetzungen, muß aber nur
hat man stärkere
Vorraussetzungen, muß aber nur 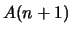 zeigen:
zeigen:
Feststellung 1.2.10 (Schluß
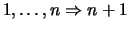
)
Für alle
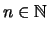 sei eine Aussage
sei eine Aussage 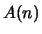 gegeben. Es gelte:
gegeben. Es gelte:
- Induktionsanfang:
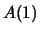 ist richtig .
ist richtig .
- Induktionsschritt:
- Für alle
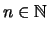 gilt der Schluß:
gilt der Schluß:
Dann ist
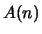
für alle
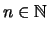
richtig.
Bezeichnung (
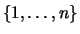 )
)
Es sei
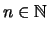 . Wir schreiben zur Abkürzung:
. Wir schreiben zur Abkürzung:
Anmerkung. Manchmal schreibt man auch suggestiver
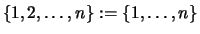
.

Man beachte aber, daß im Falle 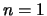 dann
dann
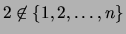 ist!.
ist!.
Eine äquivalente Formulierung des Induktionsprinzip ist:
Feststellung 1.2.11 (
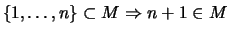
)
Es sei
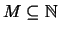 ein Menge mit den Eigenschaften
ein Menge mit den Eigenschaften
- Induktionsanfang:
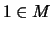
- Induktionsschritt:
-
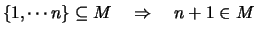
Dann folgt
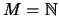
.
Man benutzt das Induktionsprinzip bei der rekursiven Definition einer Funktion
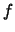 , die für alle natürlichen Zahlen erklärt werden soll:
, die für alle natürlichen Zahlen erklärt werden soll:
Feststellung 1.2.12 (rekursive Definition)
- Anfangswert:
- Man gebe den Wert
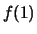 an.
an.
- Rekursion:
- Man gebe eine Vorschrift an, wie aus den Werten
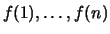 der Wert
der Wert 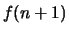 zu bilden ist.
zu bilden ist.
Dann ist
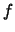
auf ganz
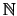
erklärt.
Bemerkung. 1. Manchmal beginnt die rekursive Definition auch mit einem Anfangswert
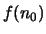 für ein
für ein
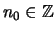 .
.
2. Die Herleitung des Rekursionsprinzips aus dem Induktionsprinzip
ist nicht so einfach
(vgl. [VAN DER WAERDEN]).




Nächste Seite: Fakultät, Binomialkoeffizient
Aufwärts: Vollständige Induktion
Vorherige Seite: Induktionsprinzip
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() zu formulieren:
zu formulieren:
![]() . Für
. Für
![]() mit
mit
![]() sei eine Aussage
sei eine Aussage ![]() gegeben. Es gelte:
gegeben. Es gelte:
![]() die folgende Aussage
zu beweisen:
die folgende Aussage
zu beweisen:
![]() sei eine Aussage
sei eine Aussage ![]() gegeben. Es gelte:
gegeben. Es gelte:
![]() )
)
![]() . Wir schreiben zur Abkürzung:
. Wir schreiben zur Abkürzung:
![]() dann
dann
![]() ist!.
ist!.
![]() ein Menge mit den Eigenschaften
ein Menge mit den Eigenschaften
![]() , die für alle natürlichen Zahlen erklärt werden soll:
, die für alle natürlichen Zahlen erklärt werden soll:
![]() für ein
für ein
![]() .
.