



Nächste Seite: Folgen
Aufwärts: Reellwertige Funktionen
Vorherige Seite: Reellwertige Funktionen
Inhalt
Eine Abbildung
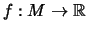 mit Zielbereich
mit Zielbereich
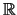 heißt auch
Funktion. Für Funktionen
heißt auch
Funktion. Für Funktionen 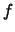 ,
, 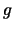 lassen sich
Summe, Produkt, und Quotient punktweise
für
lassen sich
Summe, Produkt, und Quotient punktweise
für 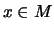 definieren:
definieren:
wobei
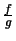 nur auf
nur auf
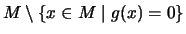 erklärt
ist.
erklärt
ist.
Entsprechend definiert man
und 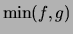 .
Weiter hat man die punktweisen Beziehungen
und
.
Weiter hat man die punktweisen Beziehungen
und
Definition 1.4.1
Eine Menge
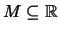
heißt
- a)
- nach oben beschränkt, falls
- b)
- nach unten beschränkt, falls
- c)
- beschränkt, falls
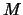 nach unten und nach oben
beschränkt ist.
nach unten und nach oben
beschränkt ist.
Die
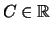 , die a) bzw. b) erfüllen heißen obere, bzw.
untere Schranke von
, die a) bzw. b) erfüllen heißen obere, bzw.
untere Schranke von 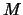 .
.
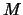 ist genau dann beschränkt, wenn ein reelles
ist genau dann beschränkt, wenn ein reelles 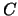 existiert, so daß
für alle
existiert, so daß
für alle 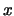 aus
aus 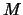 gilt
gilt
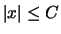 .
.
Wichtige Teilmengen von
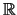 sind beschränkte oder
unbeschränkte Intervalle:
sind beschränkte oder
unbeschränkte Intervalle:
Das Symbol 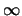 für ,,unendlich`` steht hier, wie im folgenden,
lediglich als Abkürzung.
für ,,unendlich`` steht hier, wie im folgenden,
lediglich als Abkürzung.
Die Beschränktheitsbegriffe für Mengen lassen sich auf Funktionen
übertragen, in dem man sie auf die Bilder der Funktionen anwendet.
Definition 1.4.4
Sei
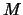
eine Menge.
- Eine Funktion
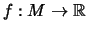 besitzt
ein Minimum, falls
besitzt
ein Minimum, falls 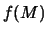 ein Minimum besitzt.
Punkte
ein Minimum besitzt.
Punkte 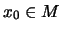 mit
heißen Minimalstellen.
mit
heißen Minimalstellen.
- Eine Funktion
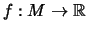 besitzt
ein Maximum, falls
besitzt
ein Maximum, falls 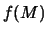 ein Maximum besitzt.
Punkte
ein Maximum besitzt.
Punkte 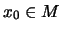 mit
heißen Maximalstellen.
mit
heißen Maximalstellen.
Maximalstellen und Minimalstellen nennen wir auch Extremalstellen.
Für Funktionen mit
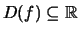 führt man folgende
Monotoniebegriffe ein:
führt man folgende
Monotoniebegriffe ein:
Bemerkung 1.4.7
Im Fall
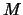
,
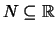
nennt man die Umkehrabbildung
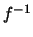
der Funktion
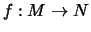
auch
Umkehrfunktion.
Dieser Satz gilt sinngemäß auch für streng monoton fallende Funktionen.




Nächste Seite: Folgen
Aufwärts: Reellwertige Funktionen
Vorherige Seite: Reellwertige Funktionen
Inhalt
Analysis1-A.Lambert
2001-02-09
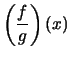
![]() ist genau dann beschränkt, wenn ein reelles
ist genau dann beschränkt, wenn ein reelles ![]() existiert, so daß
für alle
existiert, so daß
für alle ![]() aus
aus ![]() gilt
gilt
![]() .
.
![]() sind beschränkte oder
unbeschränkte Intervalle:
sind beschränkte oder
unbeschränkte Intervalle:
![]() führt man folgende
Monotoniebegriffe ein:
führt man folgende
Monotoniebegriffe ein: