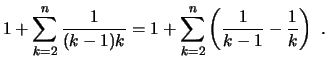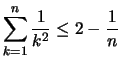Eine Funktion
![]() heißt Folge. Die Funktionswerte
heißt Folge. Die Funktionswerte
![]() heißen Folgenglieder. Man schreibt
die Folge
heißen Folgenglieder. Man schreibt
die Folge ![]() in der Form:
in der Form:
Eine Funktion
![]() heißt Folge. Die Funktionswerte
heißt Folge. Die Funktionswerte
![]() heißen Folgenglieder. Man schreibt
die Folge
heißen Folgenglieder. Man schreibt
die Folge ![]() in der Form:
in der Form:
Bei einer Folge kommt es auf die Reihenfolge der Folgenglieder an.
Man unterscheide die Folge ![]() und ihre Bildmenge
und ihre Bildmenge
![]() .
.
Allgemeiner nennt man eine Abbildung
![]() eine Folge in der
Menge
eine Folge in der
Menge ![]() und spricht im Fall
und spricht im Fall
![]() von reellen Folgen.
von reellen Folgen.
Beispiele: (Folgen)
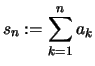
bilden. Die Folge
![]() nennt man auch eine (unendliche)
Reihe und die
nennt man auch eine (unendliche)
Reihe und die
![]() die Summanden der Reihe.
die Summanden der Reihe.
Eine Folge ![]() heißt monoton wachsend, wenn
heißt monoton wachsend, wenn
![]() für alle
für alle
![]() gilt und streng monoton wachsend, wenn ....
gilt und streng monoton wachsend, wenn ....
Eine Folge von Partialsummen
![]() (
(
![]() )
ist monoton wachsend, wenn die Summanden
)
ist monoton wachsend, wenn die Summanden
![]() sind.
sind.
| Anfangswerte: | ||||
| Rekursion: |
|
|
|
|
| 2 | 1,5 | 1,25 |
| 3 | 1,833 | 1,3611 |
| 5 | 2,2833 | 1,46361 |
| 10 | 2,92897 | 1,54977 |
| 100 | 5,18738 | 1,63498 |
| 10000 | 9,78761 | 1,64483 |
|
|
14,39272672 | 1,6449331 |
|
|
23,60306659 | 1,6449340 |
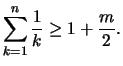
Anmerkung: Dies wurde zum erstenmal um 1350 von Nicole ORESME - Bischhof von Lisieux - gezeigt.
Da
![]() anschaulich unbeschränkt ist - dies werden wir auch noch
als Axiom formulieren - ist die Folge
anschaulich unbeschränkt ist - dies werden wir auch noch
als Axiom formulieren - ist die Folge
![]() unbeschränkt.
unbeschränkt.
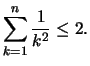
Zum Beweis siehe Vorlesung oder [KABALLO, S. 33].
Beweis .
Wir geben hierfür zwei Beweise: